基本介紹
- 中文名:等分圓周
- 外文名:circumference in equal parts
- 所屬學科:數學
- 所屬問題:平面幾何(圓)
- 相關人物:高斯(C.F.Gauss)
- 相關概念:費馬數
簡介


等分圓周問題

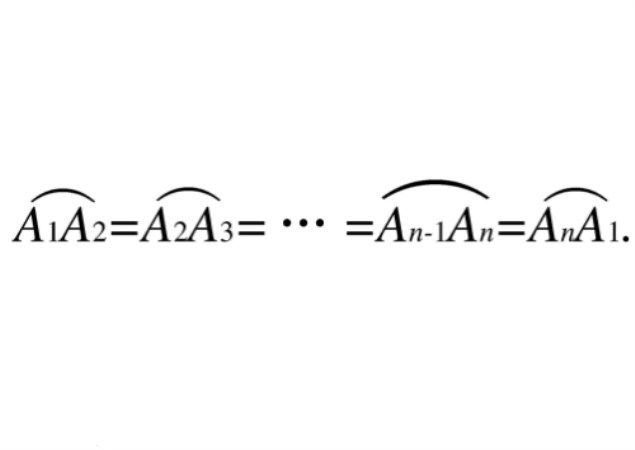



等分圓周是指利用直尺和圓規將圓周n等分,這是一個古老的數學問題。古代希臘數學家利用尺規作圖可將圓周分成3,4,5,15等分,並進而將分點逐次倍增,將圓周無限等分。高斯(Gauss,1777-1855)曾證明可用尺規作圖將...
(wantzel,p. - l.)在1837年首次給出的.到目前為止,人們只知道5個費馬素數:3,5,17,257,65537.因此,在高斯條件中所含的不同費馬素數的個數t鎮5.圓周3,5等分在古希臘時代已解決.圓周17等分是高斯在 1796年3月29日獲得的....
五等分圓周,是一種分割圓形的方法,包含尺規作圖法、單規作圖法等。等分圓周方法 作法(一):單規作圖法--只能用圓規, 不能用直尺 以 O 為圓心, a 為半徑作一個圓.⑴ 以 a 為半徑在圓上相繼取相等的弧 AB, BC, CD 和 DE...
用圓規直尺等分圓周問題(problem of dividingthe circumference with ruler and compasses)是幾何學歷史中的一個問題。能僅用圓規直尺把圓周n等分,若且唯若n是如下形式的整數:1. n=2'''gym為大於1的(正整數).2. n=2''',p,...
1801年,高斯證明:如果k是質數的費馬數,那么就可以用直尺和圓規將圓周k等分。高斯本人就是根據這個定理作出了正十七邊形,解決了兩千年來懸而未決的難題。道理 當時,如果高斯的老師告訴了高斯這是道2000多年沒人解答出來的題目,高斯...
利用六等分圓周的方法可以求得2a,3a,4a……na……。我們可以利用下面的方法求a/n,在圓(O,na)取點A作圓(A,AB=a),交點為B,B1。再作菱形BAB1O1,得AO1=a/n。至此,我們可作一條已知線段的任意有理數倍數。已知線段...
定理1 以⊙O(R)的半徑OA為直徑作半圓,三等分OA於B、C,自B、C引OA的垂線交所作半圓於D、E(圖1),則以O為圓心,各過D和E點的兩圓周必三等分原圓⊙O(R)的面積。定理2 甲乙兩多邊形彼此相似,假設甲形外切於某圓,乙形和...
■四等分圓周 只準許使用圓規,將一個已知圓心的圓周4等分.這個問題傳言是拿破崙·波拿巴出的,向全法國數學家的挑戰。簡史 中國古代 “規”就是圓規,是用來畫圓的工具,在我國古代甲骨文中就有“規”這個字。“矩”就像木工使用的...
我們知道,1/3-1/5=2/15,所以,我們所到達的正三角形頂點與正五邊形頂點之間的弧長是2/15圓周。我們只需將這段弧長一分為二,就可以得到1/15圓周。而二等分圓周是可以用尺規作圖完成的。在得到1/15圓周之後,從任意一點開始截取...
更為數學家所關注,它的出現,不僅解決了許多數學難題(如:十等分、五等分圓周;求18度、36度角的正弦、餘弦值等),而且還使優選法成為可能。優選法是一種求最最佳化問題的方法。如在煉鋼時需要加入某種化學元素來增加鋼材的強度,假設...
§3.11 等分圓周 §3.11.1 十等分圓周,黃金分割(外內比)§3.11.2 五等分圓周 §3.11.3 正五角星作法 §3.11.4 十五等分圓周 §3.11.5 n等分圓周 §3.12 尺規作圖不能解決的問題 第四章 立體幾何 §4.1 點與直線...
6.連線法等分直線 7.平行線法等分直線 8.二等分任意角 9.三等分直角 10.三等分銳角 11.三等分鈍角 12.四等分圓周 13.三等分圓周和六等分圓周 14.五等分圓周 15.已知邊長作正方形 16.已知邊長作正五邊形 17.七等分圓周 18.九...
任務四 等分圓周畫法 24 一、按同一弦長等分圓周 24 二、按不等弦長等分圓周 24 三、用分度頭等分圓周 25 任務五 劃線訓練 26 一、平面劃線 26 二、立體劃線 27 思考與練習 28 項目三 銼削 31 任務一 銼刀 31 一、銼刀組成 ...
31等分圓周和作正多邊形 311四、八等分圓周 312三、六等分圓周 313任意等分圓周 32斜度和錐度 321斜度 322錐度 33圓弧連線 331圓弧連線的作圖原理 332圓弧連線形式及作圖方法 34橢圓畫法 35平面圖形的畫法 351尺寸分析 352線段分析 353...
任務四 等分圓周畫法 25 一、按同一弦長等分圓周 25 二、按不等弦長等分圓周 25 三、用分度頭等分圓周 26 任務五 劃線訓練 27 一、平面劃線 27 二、立體劃線 28 思考與練習 30 項目三 銼削 32 任務一 銼刀 32 一、...
我們知道,1/3-1/5=2/15,所以,我們所到達的正三角形頂點與正五邊形頂點之間的弧長是2/15圓周。我們只需將這段弧長一分為二,就可以得到1/15圓周。而二等分圓周是可以用尺規作圖完成的。在得到1/15圓周之後,從任意一點開始截取...
Gauss氏等分圓周定理之證法提示》一文,就是一個典範.這篇“提示”簡潔明晰地剖析了證明難度較大的著名高斯等分圓周定理的證明思路及證明過程.高斯(Gauss)定理:若n=22m+1(m為零或正整數),且n為素數,則圓周可分作n等分.作者在...
平方奇觀 第16章 法萊數列 第17章 等分圓周 第18章 球戲 第19章 黃金定理 第20章 爭攀高峰 第21章 分解 第22章 佩爾方程 第23章 形態學 第24章 石城虎踞 第25章 馬上比武 第26章 女王的講解:問題的解答與提示 索引 ...
