伽利略定理(Galilei theorem)是著名的圓面積等分定理,若OA為⊙O的半徑,點M,N為OA的三等分點,以OA為直徑作半圓,且過點M,N作OA之垂線交半圓於點P,Q,則以O為圓心,OP,OQ為半徑之圓,必將最初的圓面積三等分,此定理由伽利略(G.Galilei)提出。
基本介紹
- 中文名:伽利略定理
- 外文名:Galilei theorem
- 所屬學科:數學
- 所屬問題:平面幾何(圓)
- 簡介:著名的圓面積等分定理
- 提出者:伽利略(G.Galilei)
定理介紹
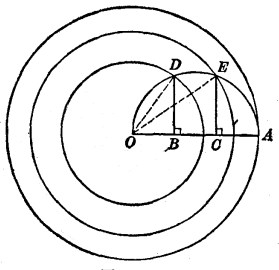
定理的證明










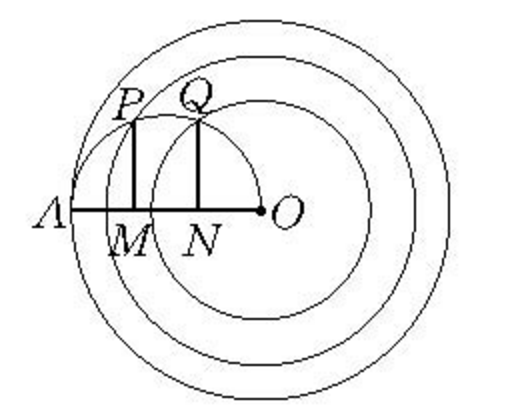
伽利略定理(Galilei theorem)是著名的圓面積等分定理,若OA為⊙O的半徑,點M,N為OA的三等分點,以OA為直徑作半圓,且過點M,N作OA之垂線交半圓於點P,Q,則以O為圓心,OP,OQ為半徑之圓,必將最初的圓面積三等分,此定理由伽利略(G.Galilei)提出。











伽利略定理(Galilei theorem)是著名的圓面積等分定理,若OA為⊙O的半徑,點M,N為OA的三等分點,以OA為直徑作半圓,且過點M,N作OA之垂線交半圓於點P,Q,則以O為圓心,OP,OQ為半徑之圓,必將最初...
伽利略還提出過合力矩定理,拋射體運動規律。在經典力學的建立上伽利略可以說是牛頓的先驅。伽利略對擺的運動作過長期的觀察和研究。在後來的研究中指出單擺的周期和擺長度的平方根成正比。這一規律為後來計時機構(擺鐘)的設計提供了根據...
在14、15世紀的歐洲,尤其是義大利,平均速度定理的奧里斯姆的幾何證明以及大量的算術證明廣為認知。在伽利略《關於兩門新科學對話》中,平均速度定律是第三天對話的頭一個命題,伽利略的證明與奧里斯姆的極為相似,甚至所用的幾何圖形都一...
牛頓第二、第三定律以及由牛頓運動定律建立起來的質點力學體系,如動量定理、動量守恆定律、動能定理等,只對慣性系成立。2.牛頓第一定律是其他原理的前提和基礎。第一定律中包含的基本概念,奠定了經典力學的概念基礎,從而使它處於理論...
該式在牛頓力學(相對論低速近似)就是動能定理。據此,稱 為相對論動能。(2)電動力學 電動力學的基礎是麥克斯韋方程組和洛倫茲力公式。麥克斯韋方程組是:在洛倫茲變換下,可以驗證,該方程組天生是協變的,無需修改;但是,引入...
伽利略的慣性原理是近代科學的起點,它摧毀了反對哥白尼的所謂缺乏地球運動的直接證據的藉口。而被現代社會所普遍認知的慣性原理,來自於牛頓的《自然哲學的數學原理》(Mathmatical Principles of Natural Philosophy, 1687),定義如下:所有物體...
動力學普遍定理是質點系動力學的基本定理,它包括動量定理、動量矩定理、動能定理以及由這三個基本定理推導出來的其他一些定理。動量、動量矩和動能是描述質點、質點系和剛體運動的基本物理量。作用於力學模型上的力或力矩,與這些物理量...
亥姆霍茲速度分解定理指出,流體微團的運動可以分解為平動、轉動和變形3部分之和(見機械運動)。流體速度分解定理同剛體速度分解定理的重要區別為:①流體微團運動比剛體的多了變形速度部分;②剛體速度分解定理對整個剛體成立,因此是整體性...
另一個在流行文化中占了很大分量的思想實驗是“無限猴子定理”,也叫做“猴子和打字機”實驗。定理的內容是,如果無數多的猴子在無數多的打字機上隨機的打字,並持續無限久的時間,那么在某個時候,它們必然會打出莎士比亞的全部著作。...
伽利略相對性原理與愛因斯坦狹義相對論原理的不同 小專欄:速度怎樣合成?第2章 時間延緩是怎么回事?1.浦島效應 2.為什麼時間會變慢?3.時間延緩也是彼此彼此 4.用算式來看時間變慢 補充說明 套用勾股定理證明時間延緩的算式 小專欄...
該定理是狹義相對性原理的推廣。在狹義相對論中,如果我們嘗試去定義慣性系,會出現死循環:一般地,不受外力的物體,在其保持靜止或勻速直線運動狀態不變的坐標系是慣性系;但如何判定物體不受外力?回答只能是,當物體保持靜止或勻速...
牛頓用第三定律來推導出動量守恆。但是,根據高等物理理論,動量守恆比第三定律更為基礎(套用諾特定理,可以從伽利略不變性推導出動量守恆)。更普遍的動量守恆並不依賴於牛頓定律。為了要證實第三定律的正確性,牛頓想出一個實驗。假設在...
為了建立極限理論的基本定理,不少數學家開始給出無理數的嚴格定義。1860年,魏爾斯特拉斯提出用遞增有界數列來定義無理數;1872年,戴德金提出用分割來定義無理數;1883年,康托爾提出用基本序列來定義無理數;等等。這些定義,從不同...
矢量動力學的基礎是由伽利略(G. Galilei)奠定的。他建立了以觀察與實驗為基礎的科學研究方法。牛頓繼續了他的工作,1687年牛頓在他的名著《自然哲學的數學原理》中對矢量動力學作了系統的敘述。據此,矢量力學又稱為牛頓力學。牛頓力學是...
其中,第1、2周介紹狹義相對論和廣義相對論的基礎知識;第3至6周介紹靜電場的物理定律、原理、定理及套用方面的知識;第7至9周介紹恆定磁場中的磁場現象、安培環路定理及套用、磁力矩及做功問題、介質磁化機制與其磁場強度的計算等知識。
他對每一個現象的都是描述性質的,對發現的每一個自然定理都是性質定義。雖然這種認識對我們認識感官世界功不可滅,但卻缺乏深入思考的基礎,因為從事物的一種性質延伸到另一種性質,往往是超出了人類的認識能力。定量分析 定量分析作為...
古希臘數學家歐幾里德把人們公認的一些幾何知識作為定義和公理(公設),在此基礎上研究圖形的性質,推導出一系列定理,組成演繹體系,寫出《幾何原本》,形成了歐氏幾何。按所討論的圖形在平面上或空間中,又分別稱為“平面幾何”與“立體...
另一個在流行文化中占了很大分量的思想實驗是“無限猴子定理”,也叫做“猴子和打字機”實驗。定理的內容是,如果無數多的猴子在無數多的打字機上隨機打字,並持續無限久的時間,那么在某個時候,它們必然會打出莎士比亞的全部著作。猴...
哥白尼用以支持他的學說的論據,主要屬於數學性質。他認為一個科學學說是從某些假說引申出來的一組觀念。他認為真正的假說或者定理必須能夠做到下面兩件事情:它們必須能夠說明天體所觀測到的運動。它們必須不能違背畢達哥拉斯關於天體運動是...
經研究與分析,所得出的一系列重要結果是:作者在書中根據坐標變換方程,不僅導出了兩事件間的相對速度公式,同時還利用相對速度公式系統地討論了不同參照系下的速度相加定理,以及調整後的伽利略速度相加定理與《相對絕對論》速度相加定理...
