在一定時間間隔內，一個點或物以與所問瞬間相同的速度勻速運動一定的距離，人們稱之為平均速度定理。
基本介紹
- 中文名：平均速度定理
- 性質：學科術語
簡介,形成過程,
簡介
14世紀早期牛津大學的梅頓學院，一群英國學者開始用與處理性質強度變化同樣的方法來處理速度或局部運動的變化。中世紀的貢獻在於創造性地正確定義了勻速和勻加速運動。在梅頓學院及其他地方，勻速運動被定義為在任何（或所有）相等的時間間隔內通過相等的距離。梅頓學院還把勻速運動的定義推廣到最簡單的變速運動，從而得出了勻加速運動的精確定義：在所有相等的任意長度的時間間隔內，獲得一個相等的速度增量。他們藉助均勻速度來定義瞬時速度：
S=1/2Vf t。S是距離，Vf終速度，t是加速的時間。Vf=at，a是加速度，替換可得這是勻加速運動距離的通常表達式
。當勻加速不是從靜止而是從某一特定速度Vo開始，中世紀的表述可寫成：S=[Vo+（Vf—Vo）/2]t，或簡單地寫成：S= Vot+1/2 a t，因為Vf —Vo=at。
形成過程
在14、15世紀，人們為這個關鍵定理提出了大量的算術和幾何證明。其中以尼古拉·奧里斯姆的幾何證明最為著名。這個證明大約於1350年提出，收在他的《論性質的構形》之中，這本著作對性質的張弛做了最富原創性的也是最完備的處理。
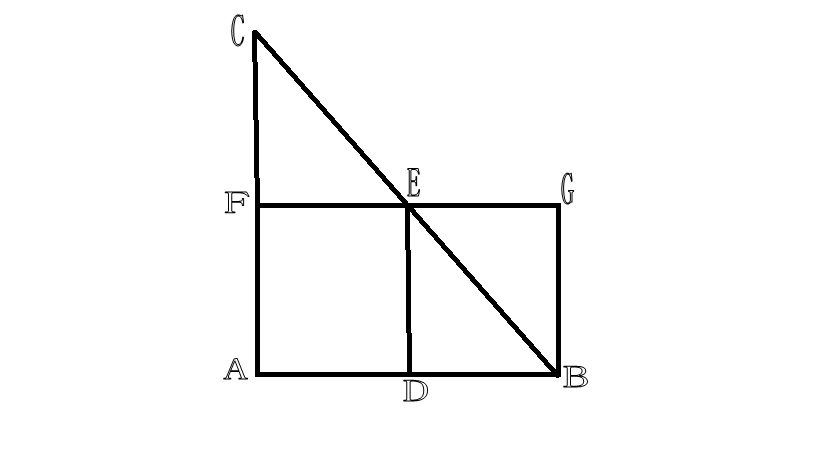
在圖中，令線AB代表時間，垂直於AB的線段代表物體Z的速度：從靜止點B開始，均勻地增大到最大速度AC。包含在三角形 CBA內的速度強度總量被構想為代表在總時間AB內Z從B出發沿直線BC到C所通過的總距離。令線段DE代表Z在沿AB時間中點測得的瞬時速度。現在，如果Z以DE處的速度勻速運動，在時間AB內從G到F沿線GF運動的總距離由長方形AFGB給出。如果能證明三角形CBA面積等於長方AFGB的面積，就證明了一個從靜止開始作勻加速運動的物體所通過的距離等於在同一時間間隔內以勻加速運動時間間隔中點的速度作勻加速運動的物體所運行的距離，即Z作勻速運動的距離S=1/2Vf t，等於Z作勻加速運動的距離 
。
在14、15世紀的歐洲，尤其是義大利，平均速度定理的奧里斯姆的幾何證明以及大量的算術證明廣為認知。在伽利略《關於兩門新科學對話》中，平均速度定律是第三天對話的頭一個命題，伽利略的證明與奧里斯姆的極為相似，甚至所用的幾何圖形都一樣，只是伽利略作了一個90°的轉向。
