簡介
在量子電動力學中,
穆勒散射(英語:Møller scattering)指
電子-電子到電子-電子的
散射過程,得名於計算出極端
相對論極限下該散射的
截面的丹麥物理學家克里斯蒂安·穆勒。該過程可以表示為:
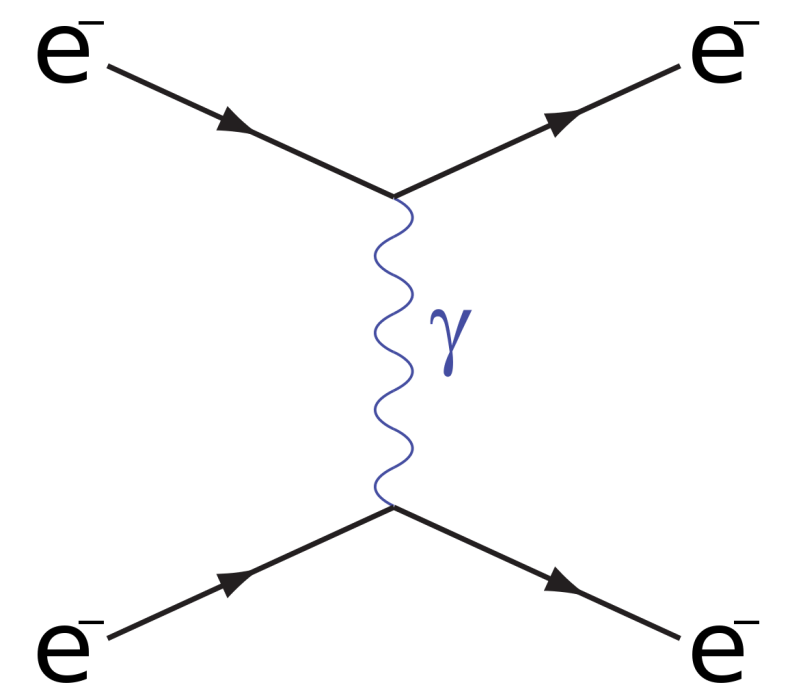
該散射截面的領頭項由t-道和u-道兩張
費曼圖貢獻,它們分別描述兩個電子交換
虛光子進而發生散射的兩個過程。穆勒散射的t-道圖和u-道圖分別與
巴巴散射(即電子-
正電子到電子正電子的散射)的s-道圖和u-道圖交叉對稱。
穆勒散射的不對稱性表示為:
其中m是電子質量,E是入射電子的能量(在另一個電子的參考系中),
是
費米常數,
是
精細結構常數,
是質量幀中心的散射角度,
是弱的混合角,也稱為Weinberg角。
散射
當傳播中的
輻射,像
光波、音波、
電磁波、或粒子,在通過局部性的位勢時,由於受到位勢的作用,必須改變其直線軌跡,這物理過程,稱為
散射。這局部性位勢稱為
散射體,或
散射中心。局部性位勢各式各樣的種類,無法盡列;例如,粒子、氣泡、液珠、液體密度
漲落、晶體缺陷、粗糙表面等等。在傳播的波動或移動的粒子的路徑中,這些特別的局部性位勢所造成的效應,都可以放在
散射理論(scattering theory)的框架里來描述。
單散射和多重散射
假若輻射只被一個局部性散射體散射,則稱此為
單散射。假若許多散射體集中在一起,輻射可能會被散射很多次,稱此為
多重散射。單散射可以被視為一個
隨機現象;而多重散射通常是比較命定性的。這是兩種散射的主要不同點。
由於單獨的散射體的位置,相對於輻射路徑,通常不會明確的知道。所以,散射結果強烈地依賴於入射軌道參數。對於觀測者,散射結果顯得相當的隨機。移動
電子朝著
原子核碰撞是一個標準案例。由於
不確定性原理,相對於電子的入射路徑,原子的確定位置是個未知數,無法準確地測量出來,碰撞後,電子的散射行為是隨機的。所以,單散射時常用
機率分布來描述
在多重散射過程里,經過眾多的散射事件,散射作用的隨機性很容易會因為平均化而被凐滅不見,輻射的最終路徑會顯示為
強度的命定性(deterministic)分布。光束穿過濃厚大霧是一個標準案例。多重散射可以與
擴散類比。在許多狀況,兩個術語可以替代使用。用來製造多重散射的光學器材,稱為
擴散器。
不是每一種單散射都是隨機地。一個完美控制的
雷射束能夠準確地散射於一個微粒,產生出命定性的結果。這樣的狀況也會發生於
雷達散射,目標大多數是
巨觀物體,像飛機或火箭。
類似地,多重散射有時也會產生很隨機的結果,特別是
相干輻射。當相干輻射被多重散射的時候,
強度會發生隨機
漲落,稱此現象為
散斑(speckle)。假若,一個相干輻射的不同部分散射於不同的散射體,則也會產生散斑。在某些罕見的狀況,多重散射的散射次數並不多,隨機性並沒有被平均化凐滅。學術界公認,這類系統很不容易精確地模型化。
散射的主要研究問題,時常涉及到預測各種系統怎樣散射輻射。給予足夠的計算資源和系統信息,這些問題大都可以解析。一個廣泛研究,更加困難的挑戰是逆散射問題(inverse scattering problem)。這問題主要研究的是,從觀測到的散射行為,來決定入射輻射或散射體的性質。一般而言,解答不是唯一的;不同的散射體可以給予同樣的散射樣式。幸運地,科學家找到一些方法,來萃取許多關於散射體的資料。雖然這些資料並不完全,但還是相當有用。這些方法廣泛的用於感測和
計量學(metrology)。
許多科技領域顯著地套用到散射和散射理論。例如,雷達感測、
超音波檢查、
半導體晶片檢驗、
聚合過程監視、電腦成像等等。
電磁散射
大多數物體都可以被看見,主要是因為兩個物理過程:光波散射和光波吸收。有些物體幾乎散射了所有入射光波,這造成了物體的白色外表。光波散射也可以給予物體顏色。例如,不同
色調的藍色,像天空的天藍、眼睛的
虹膜、鳥的羽毛等等。奈米粒子的共振光波散射會產生不同的高度飽和的,生動的
色相,特別是當涉及
表面電漿共振(surface plasmon resonance)。
在
瑞利散射里,電磁輻射(包括光波)被一個小圓球散射。圓球可能是一個粒子、泡沫、水珠、或甚至於密度漲落。物理學家瑞利勳爵最先發現這散射效應的正確模型,因此稱為
瑞利散射。為了要符合瑞利模型的要求,圓球的直徑必須超小於入射波的
波長,通常上界大約是波長的1/10。在這個尺寸範圍內,散射體的形狀細節並不重要,通常可以視為一個同體積的圓球。當陽光入射於大氣層時,氣體分子對於陽光的瑞利散射,使得天空呈現藍色。這是根據瑞利著名的方程:
陽光的藍色光波部分波長比較短,散射強度比較大;而紅色光波部分波長比較長,散射強度比較小。
外太空的輻射通過地球大氣層時,衰減的主要原因是輻射吸收和瑞利散射。散射的程度變化是粒子直徑與波長比例的
函式,連同許多其它因子,像
極化、角度、以及
相干性等等。
瑞利散射不適用於直徑較大的散射體。德國物理學家古斯塔夫·米最先找到這問題的解答。因此,大於瑞利尺寸的圓球的散射被稱為
米氏散射。在米氏區域內,散射體的形狀變的很重要。這理論只能用在類球體。
瑞利散射和米氏散射都可以被視為彈性散射,光波的能量並沒有大幅度地改變。可是,移動的散射體所散射的電磁波會產生
都卜勒效應,能量會稍微改變。這效應可以被用來偵測和測量散射體的速度,可以套用於光達(LIDAR)和
雷達這一類科技儀器。
當粒子直徑與波長比例大於10的時候,
幾何光學的定律可以用來描述光波與粒子的相互作用。在這裡,通常不稱這相互作用為散射。
對於一些瑞利模型和米式模型不適用的案例,像不規則形狀粒子,有很多種不同的數值計算方法可以讓我們選擇使用,求算散射的解答。最常見的方法是有限元方法。此法解析
麥克斯韋方程組,尋求散射的電磁場的分布。程式工程師特別設計出複雜的軟體,專門計算這類問題。只需要使用者給出散射體的折射率或折射率函式,電腦就可以計算出電磁場結構的二維或三維模型。假若結構比較龐大複雜,則可能需要高功能電腦大量的運算時間,才能得到結果。
另外一種特別的電磁散射是
相干回散射(backscatter)。這是一個相當不為人知的現象。當相干輻射(像雷射光束)傳播通過一個擁有很多散射體的介質時,電磁波會被散射很多次。一個代表性的多重散射介質例子是濃厚雲塊。朝著原本入射方向的反方向,相干回散射效應會產生一個非常大的峰值強度。實際上,一般的電磁波很大部分都會散射回去。對於非相干輻射,散射通常會在反方向產生一個局部最大值。可是,相干輻射的峰值強度是非相干輻射的兩倍。測量這些數值是很困難的。原因有兩個。第一個原因是,直接地測量回散射同時也會阻擋入射電磁波。但是,科學家已經想出精巧的方法來克服這問題。第二個原因是,強度峰通常會是非常的尖銳。偵測器必須擁有非常高的角解析度,才能夠看到峰值,不會將強度峰值與鄰近的低強度值平均起來。
基本信息
虛粒子(virtual particle),意即虛構粒子、假想粒子,是在量子場論的數學計算中建立的一種解釋性概念,指代用來描述
亞原子過程例如撞擊過程中粒子的數學項。但是,虛粒子並不直接出現在計算過程的那些可觀測的輸入輸出量中,那些輸入輸出量只代表實粒子。虛粒子項代表那些所謂離質量殼(off mass shell)的粒子。例如,它們沿時間反演、能量不守恆、以
超光速移動,每條看起來都和物理基本原理相悖。虛粒子發生在那些大致可被實輸出量相消的組合項中,因此才產生了前述那些不實的衝突。虛粒子的虛“事件”通常看起來是一個緊接著另一個發生,例如在一次撞擊的時長中,所以他們顯得短命。如果在計算中略去那些被詮釋為代表虛粒子的數學項,計算結果將變成近似值,有可能較大地偏離完整計算得到的正確而且精確的結果。
量子理論不同於經典理論。區別在於對於亞原子過程的內部機制的計算。經典物理不能處理這種計算。
海森堡認為,在
亞原子過程例如碰撞中,到底“實際上”“真正”發生了什麼,是不可直接觀測的,也沒有可用以描述的單一而且物理明確的圖像。
量子力學具有這樣的特質:即它可以避開關於內部機制的思考。它把自己限制在那些實際上可觀測可感知的方面。但是,虛粒子則是一種概念化的手段,通過給
亞原子過程的內在機制提供假設性的詮釋性圖像,它試圖繞過
海森堡的洞察。
虛粒子不必具有和對應實粒子相等的
質量。這是因為它短命而且瞬變,所以
不確定性原理允許它不必守恆
能量和
動量。虛粒子存活得越久,它的特徵就越接近實粒子。
理論
由於
測不準原理,虛粒子的
能量與
動量都是不確定的。虛粒子也有一些和實粒子(real particle)相同的特性,像是遵守
守恆定律。如果一個單一的粒子被偵測到,那代表了它存在的時間長到了使它不可能成為虛粒子的程度,即虛粒子是不可能被觀測到的。
虛粒子被用來描述那些無法用實粒子來描述的基本互動作用力的
量子,
靜力場就是其中一個例子,像是
電場或
磁場,或是任何一種場,都無法以光的速度從一個位置來攜帶訊息至另一個位置(藉由場來傳播的資訊必須由實粒子來當載子)。
虛光子也是一種近場的主要載子,而這種
近場是一種短距的效應,而且不會擁有像電磁波的光子那樣的特色。舉個例子來說,當能量從纏繞的變壓器到另一台變壓器,或到
MRI的掃描器上時,就量子而言這種攜帶能量的是虛光子而不是實光子。
虛粒子是由無質量的粒子所組成,像是
光子,但虛粒子也是可能有質量的且被稱之為
離殼。因為它們只存在極短的時間裡面(稱之為有限的"range"),所以這些虛粒子被允許擁有質量。這是根據
不確定原理而來的,不確定原理允許粒子的能量乘上它們存在的時間小於
普朗克常數即可。擁有質量更使得了單一的虛粒子更容易從帶電的基本粒子被創造和射出,而這對於無質量的光子在沒有違反能量跟動量守恆之下是不可能發生的(單一的實粒子要被創造或射出必定是擁有兩個以上粒子的系統)。對於那些有真正有質量的粒子,它們的虛態仍然會破壞狹義相對論理的能量動量關係,有質量的粒子基本上都會利用以下的關係來預測:
通常力的載子都是無質量的,主要的例外就是
弱作用力中的W/W和Z
玻色子。
虛粒子的概念很接近量子波動的想法。虛粒子可以被想成是進入一種實體的量,就像是電場一般,而這個量是在量子力學所要求的期望值附近擾動。
參閱