矩形切割主要用於解決有重疊部分的面積計算問題，在解決信息學競賽的一些題目時有很高的效率。矩形切割是一種處理平面上矩形的統計的方法，它的原型是線段切割，可以拓展到三維的立方切割。
基本介紹
- 中文名：矩形切割
- 外文名：Rectangle cutting
- 套用學科：計算機科學
- 適用領域範圍：重疊面積計算
解釋,主要程式,例子,
套用學科：計算機科學
解釋
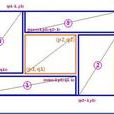
矩形切割主要解決有重疊部分的面積計算問題。
矩形切割是一種處理平面上矩形的統計的方法。
許多統計類的問題通過數學建模後都能轉化為用矩形切割來解決。矩形切割的原型是線段切割，可以拓展到三維的立方切割。
（1）線段切割
（2）矩形切割
（3）立方切割
主要程式
procedure cal(l,r,b,t,z:longint);
begin
while (z<=n)and((l>x2[z])or(r<x1[z])or(b>y2[z])or(t<y1[z]))do inc(z);
if z>n then
begin
inc(col[now],(r-l+1)*(t-b+1));
exit;
end;
if l<x1[z] then
begin
cal(l,x1[z]-1,b,t,z+1);
l:=x1[z];
end;
if r>x2[z] then
begin
cal(x2[z]+1,r,b,t,z+1);
r:=x2[z];
end;
if t>y2[z] then
begin
cal(l,r,y2[z]+1,t,z+1);
t:=y2[z];
end;
if b<y1[z] then
begin
cal(l,r,b,y1[z]-1,z+1);
b:=y1[z];
end;
end;
procedure work;
var
i,j,k:longint;
begin
x1[0]:=1;
y1[0]:=1;
x2[0]:=a;
y2[0]:=b;
color[0]:=1.0;
for i:=n downto 0 do
begin
now:=color[i];
cal(x1[i],x2[i],y1[i],y2[i],i+1);
end;
for i:=1 to 1000 do
if col[i]>0 then
writeln(i,' ',col[i]);
end;
例子
衛星覆蓋
SERCOI（Space-Earth Resource Cover-Observe lnstitute）是一個致力於利用衛星技術對空間和地球資源進行覆蓋觀測的組織。他們研製成功一種新型資源觀測衛星-SERCOI-308。這種衛星可以覆蓋空間直角坐標系中一定大小的立方體空間，衛星處於該立方體的中心。
其中（x,y,z）為立方體的中心點坐標，r為此中心點到立方體各個面的距離（即r為立方體高的一半）．立方體的各條邊均平行於相應的坐標軸。我們可以用一個四元組(x,y,z,r)描述一顆衛星的狀態，它所能覆蓋的空間體積 。
由於一顆衛星所能覆蓋的空間體積是有限的，因此空間中可能有若干顆衛星協同工作。它們所覆蓋的空間區域可能有重疊的地方，如下圖所示（陰影部分表示重疊的區域）。
寫一個程式，根據給定的衛星分布情況，計算它們所覆蓋的總體積。
輸入輸出
輸入檔案是INPU.TXT。檔案的第一行是一個正整數N（1<=N<=10O）：表示空間中的衛星總數。接下來的N行每行給出了一顆衛星的狀態，用空格隔開的四個正整數x,y,z,r依次表示了該衛星所能覆蓋的立方體空間的中心點坐標和半高，其中-1000<=x,y,z<=1000, 1<=r<=200。
輸出檔案是OUTPUT.TXT。檔案只有一行,包
括一個正整數，表示所有這些衛星所覆蓋的空間總體積。
樣例
INPUT.TXT
3
0 0 0 3
1 –1 0 1
19 3 5 6
OUTPUT.TXT
1944
這題可以用立方體切割來做，每讀入一個立方體
(x3,y3,z3,x4,y4,z4)，就和已有的立方體(x1,y1,z1,x2,y2,z2)判斷是否有重疊，有的
話就進行切割。所有的數據處理完後就可以將全部立方體的體積加起來，就能得
出答案了。
應該注意的是新切割生成的立方體與立方體(x3,y3,z3,x4,y4,z4)是不會有重
疊部分的。因此我們在讀入矩形(x3,y3,z3,x4,y4,z4)之前，先把當前立方體集合中
的立方體總數tot 記錄起來 tot1 ← tot，那么循環判斷立方體重疊只需循環到tot1
就行了，新生成的立方體就無需與立方體(x3,y3,z3,x4,y4,z4)判斷是否重疊了。這
樣可以節省不少時間。
