基本介紹
- 中文名:相量圖
- 外文名:Phasor Diagram
- 表示:相量以及各相量之間相互關係的圖
- 規則:可省略虛軸
- 特點:直觀的描述各個正弦量的大小
介紹,相量,相量運算法則,標量相乘,微分和積分,電路定律,電力工程,
介紹
物理和工程領域中,常會使用到正弦信號(例如交流電路的分析),這時可以使用相量來簡化分析。相量(Phasor)是振幅(A)、相位(θ)和頻率(ω)均為時不變的正弦波的一個複數,是更一般的概念解析表示法的一個特例。而將正弦信號用複數表示後進行電路分析的方法稱為相量法,而在相量圖中利用矢量表示正弦交流電的圖解法稱為矢量圖法。相量法可以將這幾個參數的相互依賴性降低,使這3個參數相互獨立,這樣就能簡化特定的計算。Phasor是PhaseVector的混成詞。Phasor也被稱作復振幅,在比較古老的英文工程文獻當中,也常被寫作sinor,甚至寫作complexor。
參數中的頻率參數對正弦波的線性組合的所有分量都一樣,若利用相量法將這一因子提取出來,留下的只是振幅和相位信息的代數組合而不是三角函式的組合。同樣,線性微分方程的求解也可以通過相量法簡化為代數運算。不過因為要提取頻率,所以只有同頻率的正弦量才能進行相量運算。由此可知,相量是一種簡化的表示方法,紀錄一正弦波的振幅和相位數據。因此,相量一般指振幅和相位部分。
忽略一些數學細節,相量變換也可以看作是拉普拉斯變換的特定情況,該變換還能同時導出RLC電路的瞬態回響。然而拉普拉斯變換在數學上套用較為困難,因而在只需要進行穩態分析時沒有必要使用。
相量圖也可表述成在複平面上表示相量以及各相量之間相互關係的圖。相量圖能直觀的描述各個正弦量的大小和相互間的相位關係。利用平行四邊形法則可以進行加減運算。
為清楚起見,相量圖可省略虛軸,也可以同時省略實軸和虛軸。
為分析方便,正弦穩態電路的電壓、電流、功率、阻抗等可以用複數即相量來表示,在複平面上,它們之間的加、減運算等,就可以用相量圖解來完成。
相量
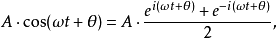
正弦波可以被理解成複平面上的旋轉矢量在實軸上的投影。這一矢量的模是振動的幅度,而矢量的幅角是總相位 。相位常數
。相位常數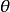 代表復矢量於
代表復矢量於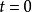 時刻與實軸的夾角。
時刻與實軸的夾角。

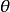
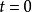
相量運算法則
標量相乘
相量 與復常數
與復常數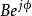 的乘積也是一個相量,這意味著相量乘法只會改變正弦波的振幅和相位。
的乘積也是一個相量,這意味著相量乘法只會改變正弦波的振幅和相位。

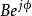
在電子學中,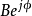 是獨立於時間的阻抗,且並不是另一相量的簡短記法。阻抗乘以相量電流可得到相量電壓。但2個相量相乘或相量乘方運算的結果表示2個正弦波的乘積,這種運算是非線性運算,會產生新的頻率分量。相量記法只能表示同一頻率的系統,例如正弦波模擬的線性系統。
是獨立於時間的阻抗,且並不是另一相量的簡短記法。阻抗乘以相量電流可得到相量電壓。但2個相量相乘或相量乘方運算的結果表示2個正弦波的乘積,這種運算是非線性運算,會產生新的頻率分量。相量記法只能表示同一頻率的系統,例如正弦波模擬的線性系統。
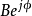
微分和積分
一個相量的時間導數或積分可以產生另一個相量,在相量表示法中,正弦波的時間導數僅需要與常數 相乘就能得到;同樣,對相量進行積分運算也只需要乘以常數
相乘就能得到;同樣,對相量進行積分運算也只需要乘以常數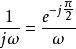 就能得到;不論是微分還是積分運算,時間變數因子
就能得到;不論是微分還是積分運算,時間變數因子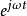 均不受影響。當利用相量法求解線性微分方程時,我們只需要將方程中全部項中的因子
均不受影響。當利用相量法求解線性微分方程時,我們只需要將方程中全部項中的因子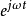 提取出來後,計算完成後將這一因子重新引入答案中,就可完成全部求解。例如,求解RC電路中電容上的電壓,可建立下列微分方程:
提取出來後,計算完成後將這一因子重新引入答案中,就可完成全部求解。例如,求解RC電路中電容上的電壓,可建立下列微分方程:

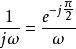
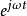
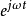
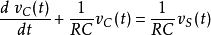
當電路中的電壓源是正弦變化時:

利用相量的簡短記法,微分方程可化簡為:
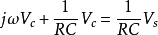
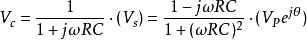
如上所示,結果為一個因子與 的乘積,這代表了關聯於
的乘積,這代表了關聯於 和
和 的
的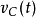 的幅值和相位的不同之處。
的幅值和相位的不同之處。



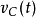
用極坐標形式表示,則結果為:
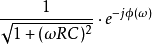
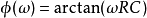
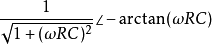
因此得到電容電壓為: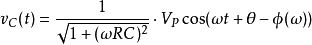 。
。
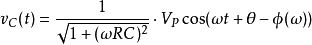
電路定律
用相量法表示正弦交流電後,就可以將直流電路的分析方法直接用於分析交流電路,這些基本定律如下:
- 基爾霍夫電路定律的複數形式也可用於相量計算中。
由以上定律,我們可以使用相量法進行阻性電路分析,可分析包含電阻、電容和電感的單一頻率交流電路。分析多頻率線性交流電路和不同波形的交流電路時,可以先將電路化為正弦波分量的組合(由疊加定理滿足),然後對每一頻率情況的正弦波進行分析,找出電壓和電流。
電力工程
在三相交流電力系統的分析中,通常會有一組相量被定義為3個復單位立方根,並以圖表示為角0°、120°以及240°處的單位幅值。將多相交流電路的量化為相量後,平衡電路可被化簡,而非平衡電路可被當作對稱電路的代數組合。這種方法簡化了電學計算中計算電壓降、功率流以及短路電流所需的工作。在電力系統分析中,相位角的單位常為度,而幅值大小則通常是以方均值而不是峰值來定義。
同步相量技術中使用數字式儀表來測量相量,先進的測量設備包括同步相量測量裝置(PMU),能直接即刻測得某節點的相量,不需要花費時間進行大量的計算。在輸電系統中,相量一般被廣泛地認為是表示輸電系統電壓。相量的微小變化是功率流和系統穩定性的靈敏指示參數。