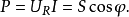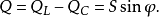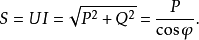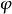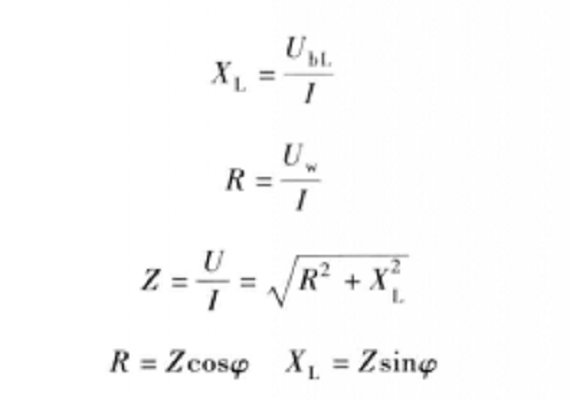在相量法分析中,經常以相量圖為輔助。利用各相量間的幾何關係,可得出電壓三角形和阻抗三角形。由於R、L、C串聯後,組成的阻抗模|Z|、電阻R、電抗X三者之間符合直角三角形的關係,由此構成的三角形稱為阻抗三角形。可知Z是一個複數,其實部為電阻,虛部為電抗。它集中地反映了電路中的三種參數對電流的阻礙作用。要注意它是阻抗的複數形式,不是時間的函式,不是正弦量,也不是相量,與電壓、電流的相量形式性質不同,只是複數計算量。用大寫字母表示時,上方不打點,畫圖表示時不帶箭頭。電壓三角形和阻抗三角形都是直角三角形,且有一個銳角相等,所以它們是相似三角形。但要注意的是,電壓三角形的三條邊都是相量,所以說是相量三角形;而阻抗三角形的三條邊都不是相量,所示說是非相量三角形。
基本介紹
- 中文名:阻抗三角形
- 外文名:impedance triangle
- 所屬學科:數理科學
- 相關概念:電阻,電抗,相量法等
- 性質:一種非相量三角形
基本介紹
 圖1RLC 串聯電路
圖1RLC 串聯電路
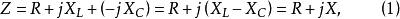
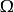
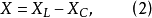
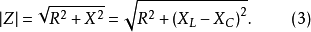

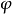
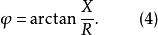
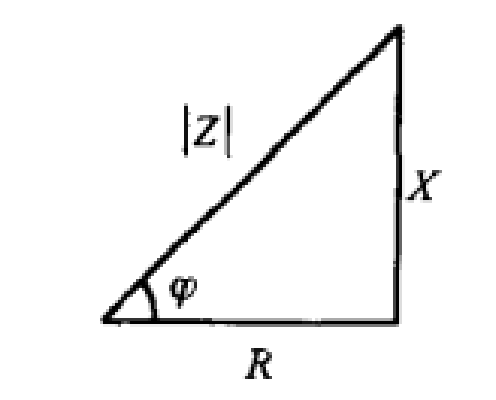 圖2 阻抗三角形
圖2 阻抗三角形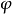
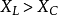
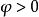
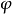
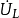

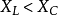

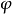

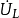
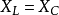
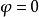
電壓三角形
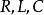
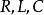

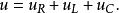
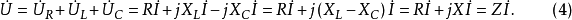

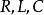
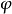
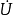

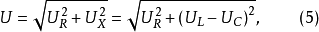
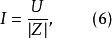
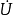


功率三角形
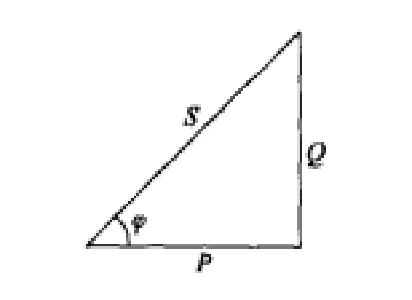 圖3
圖3