相對自由代數(relatively free algebras)是指可由自由代數的T理想決定的商代數。
自由代數是具有生成基的一類代數。集合X={x1,x2,…}中若干個元依照某個次序的一個排列,稱為X上一個字。若在X上字的全體集合中任二元h=xi1xi2…xin,g=xj1xj2…xjm,規定乘法:h·g=xi1xi2…xinxj1xj2…xjm,則此集合構成一個自由半群。
基本介紹
- 中文名:相對自由代數
- 外文名:relatively free algebras
- 領域:數學
- 性質:商代數
- 定義:由自由代數的T理想決定的商代數
- 形成方式:代數同態擴張
概念,代數,自由代數,商代數,理想,
概念
相對自由代數(relatively free algebras)是指可由自由代數的T理想決定的商代數。設I是自由代數Λ{X}的理想,商代數U=Λ{X}/I稱為相對自由的,是指對滿足U的所有恆等式即每個≤ΛU的代數R,使得映射σ:x-k→rk∈R有惟一的U→R的代數同態擴張(其中x-k=xk+I)。若U=Λ{x}/I是相對自由的,則U的恆等式集為I,因此I是Λ{x}的T理想;反之,若A是Λ{x}的T理想,則Λ{x}/A是相對自由的。
代數
設K為一交換體。把K上的向量空間E叫做K上的代數,或叫K-代數,如果賦以從E×E到E中的雙線性映射。換言之,賦以集合E由如下三個給定的法則所定義的代數結構:
——記為加法的合成法則(x,y)↦x+y;
——記為乘法的第二個合成法則(x,y)↦xy;
——記為乘法的從K×E到E中的映射(α,x)↦αx,這是一個作用法則;
這三個法則滿足下列條件:
a) 賦以第一個和第三個法則,E則為K上的一個向量空間;
b) 對E的元素的任意三元組(x,y,z),有:
x(y+z)=xy+xz(y+z)x=yx+zx;
c)對K的任一元素偶(α,β)及對E的任一元素偶(x,y),有(αx)(βy)=(αβ) (xy).
設A為一非空集合. 賦予從A到K中的全體映射之集ℱ(A,K)以如下三個法則:



則ℱ(A, K)是K上的代數, 自然地被稱為從A到K中的映射代數.當A=N時, 代數ℱ(A,K)叫做K的元素序列代數。
無論是在代數還是在分析中,代數結構都是最常見到的結構之一。十九世紀前半葉末,隨著哈密頓四元數理論的建立,非交換代數的研究已經開始。在十九世紀下半葉,隨著M.S.李的工作,非結合代數出現了。到二十世紀初,由於放棄實數體或複數體作為運算元域的限制,代數得到了重大擴展。
與外代數,對稱代數,張量代數,克利福德代數等一起,代數結構在多重線性代數中也建立了起來。
自由代數

規定:

則Λμ(X)構成一個結合代數,稱為X上自由Λ代數,記為Λ{X}。.Λ{X}中元稱為多項式。設:

αh稱為h的係數,αnh稱為單項式,且f的次數:
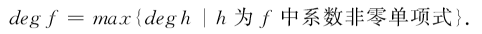
當μ(X)為交換自由么半群時,自由代數Λ[X]與Λ上多項式代數Λ{X}一致。一般地,若在自由么半群μ(X)上規定一個關係~:
xi1xi2…xin~xj1xj2…xjm,
若且唯若n=m且集合{xik|k=1,2,…,n}與集合{xjk|k=1,2,…,m=n}相等,則~為μ(X)的一個等價關係,從而可將μ(X)中元按等價分類,xi1xi2…xin所在的類用表示,且記:
μ-(X)={|xi1xi2…xin∈μ(X),
i1≤i2≤…≤in},
於是,μ-(X)對μ(X)所誘導的乘法也構成交換么半群,也為自由么半群。同前類似,由μ-(X)所生成的Λ代數Λμ-(X)稱為自由交換代數,記為Λ[ξ].當Λ是整數環Z時,自由代數Z{X}與自由交換代數Z[ξ]分別稱為自由環與自由交換環,它們中的元素皆為整係數多項式。
商代數
商代數是一個代數結構模它的同餘關係產生的新的代數結構。
集A上的等價關係~將A劃分成互不相交的等價類的並,記成=A/~,即的元素[a]是a所在的等價類。稱為A關於~的商集。進一步,設~是代數結構〈A,◦〉上的等價關係,並且對任意a,b∈A,若a~b,對任何c∈A,都有a◦C~b◦c,且c◦a~c◦b,則稱等價關係~是〈A,◦〉上的同餘關係例如,模m同餘,a≡b (modm),若且唯若m| (a-b),是〈Z,+〉上的一個同餘關係,並且模m同餘也是〈Z,+,·〉上的同餘關係又如,群〈G,·〉的正規子群N確定的陪集關係R,aRb若且唯若ab∈N,是〈G,+〉上的同餘關係。
設~是代數結構〈A,◦〉上的同餘關係,則可在商集=A/~上定義運算*.。
[a1] * [a2]=[a1·a2]
稱代數結構〈A/~,*)=〈,* 〉為〈A,◦〉(關於~)的商代數。
一個代數結構必定與它的商代數同態,把任一元素對應到這個元素所在的等價類的映射就是代數結構到其商代數的同態映射。反過來,代數結構A的任何一個同態映射可以導出A的一個同餘關係~,並得到商代數A/~,A/~必與A的同態象同構。
理想
理想是集合論中的基本概念之一。設S為任意集合,若I⊆P(S)且滿足:
1.∅∈I;
2.若X,Y∈I,則X∪Y∈I;
3.若X,Y⊆S,X∈I,Y⊆X,則Y∈I;
則稱I為集合S上的理想.理想的概念在現代數學的幾乎每個分支中均有套用,且有許多變體或引申.例如,布爾代數上的理想即為集合上的理想的一種變體.設B為任意布爾代數,若B的一個子集I滿足:
1.0∈I,1∉I(其中0,1分別為布爾代數B中的零元與么元);
2.對任何u∈I,v∈I,有u+v∈I;
3.對任何u,v∈B,若u∈I且v≤u,又v∈I;
則稱I為B上的理想。
