基本介紹
- 中文名:相反多項式
- 外文名:opposite polynomial
- 所屬學科:數學
- 所屬問題:初等代數(多項式)
- 簡介:兩個多項式的和恆等於零
基本介紹
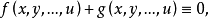
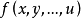
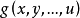
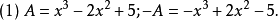
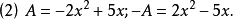
相關分析
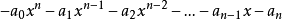
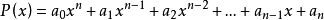
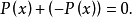
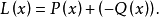
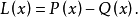
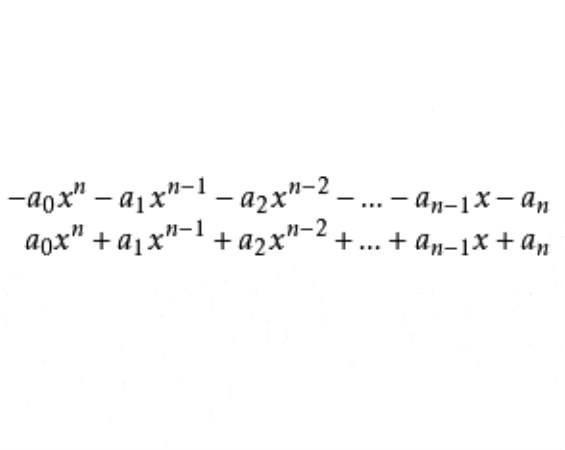
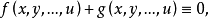
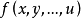
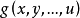
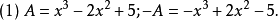
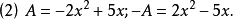
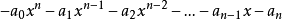
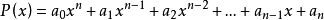
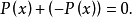
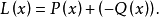
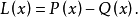
相反多項式(opposite polynomial)是相反數概念的推廣。如果兩個多項式的和恆等於零,那么這兩個多項式就叫做互為相反多項式。若以標準形式給出的兩個多項式互為相反...
在數學中,由若干個單項式相加組成的代數式叫做多項式(若有減法:減一個數等於加上它的相反數)。多項式中的每個單項式叫做多項式的項,這些單項式中的最高項次數,就...
二次多項式是指這個多項式的項數超過1,且最高次方數為2的多項式。在數學中,由若干個單項式相加組成的代數式叫做多項式(若有減法:減一個數等於加上它的相反數)。...
在編碼理論中,多項式碼(英語:polynomial code)是有效碼字集合是由多項式(通常是固定長度的多項式)可以被特定多項式(長度較短,稱為生成多項式)整除的一種線性碼。...
通常人們會使用冪級數展開式的形式來描述光學系統的像差。由於澤尼克多項式和光學檢測中觀測到的像差多項式的形式是一致的,因而它常常被用來描述波前特性。但這並不...
多項式對非確定多項式(P對NP,P versus NP)是指1971年Leonid Levin和Stephen Cook提出的一個關於容易解答的問題(p型)以及相反的難以解答的問題(NP型)的數學理論...
多項式分裂域(splitting field of a polynomial )與多項式相關的一種域。在抽象代數中,具有域中係數的多項式分裂域是該域的最小域延伸,多項式在該域上分裂為線性...
多項式被另一多項式整除,後者即是前者的因式,如果多項式 f(x) 能夠被整式 g(x) 整除,即可以找出一個多項式 q(x) ,使得 f(x)=q(x)·g(x),那么g(x) ...
笛卡爾符號法則由笛卡爾首先提出,用於分析高次多項式正根與負根的個數。...... 首先提出,用於分析高次多項式正根與負根...1(兩個)和-1,正好和原多項式的根相反...
把一個多項式在一個範圍(如實數範圍內分解,即所有項均為實數)化為幾個整式的積的形式,這種式子變形叫做這個多項式的因式分解,也叫作把這個多項式分解因式。...
