相伴定理(adjoint theore m)是關於函子Hom和②的重要定理.若A與B為兩個環，M是一個左B右A雙模，N為左B模，E是左A模，則有群同構。
相伴定理
相伴定理
相關詞條
- 相伴定理
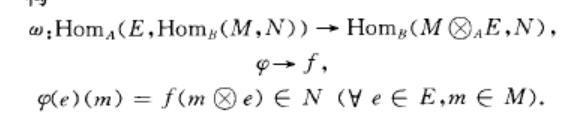
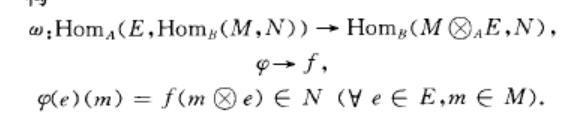
相伴定理(adjoint theore m)是關於函子Hom和②的重要定理.若A與B為兩個環，M是一個左B右A雙模，N為左B模，E是左A模，則有群同構。...
- 意志強度定理
意志強度定理是指要讓他人做好的工作，很少是一蹴而就的，在大多數情況，都不免有艱難險阻相伴。只有付出艱辛和努力，戰勝了這些艱難險阻才能達成做好工作的目的。人在某一行為活動上的努力程度，與這一行為活動所能帶來的自我肯定的多少成正比，與他對這一自我肯定評價的高低成正比。簡介 意志強度定理——管理學第...
- 亞純函式值分布理論(亞純函式理論的分支)
其他成就包括創立了調和測度與相伴原理，以及哈達馬三圓定理的推廣、彈道的測定等。奈望林納一生在許多不同論題上不斷地寫了大量的文章與書，寫有名著《解析函式論》(1936，有多種文字譯本)、《皮卡-波萊爾定理與亞純函式理論》(1929)及《單值解析函式》(1935)、《單值化》(有中譯本)、《黎曼曲面》(1953)、《...
- 貝葉斯邏輯
貝葉斯定理也稱貝葉斯推理，早在18世紀，英國學者貝葉斯(1702～1761)曾提出計算條件機率的公式用來解決如下一類問題：假設H[,1],H[,2]…互斥且構成一個完全事件，已知它們的機率P(H[,i],i=1,2,…)，現觀察到某事件A與H[,1],H[,2]…相伴隨而出現，且已知條件機率P(A/H[,i])，求P(H[,i]/A)。貝...
- 層同態
定理1 是拓撲空間X上的層，它與它的相伴空間的截影層 是同構的。定理2設 和 是拓撲空間X上的兩個層， 和 分別是它們的相伴空間，如果 和 是層同構的，則相伴空間 和 是同構的。定理3設 和 分別是拓撲空間X上的兩個層所對應的相伴空間，如果 和 是相伴空間同構，則它們對應的截影層...
- 改變人生最重要的120個定律
贏家通吃 坎特法則——管理從尊重開始 手錶定理——“雙重標準”不可行 不值得定律——不值得做的事就不值得做好 彼得原理——好員工不等於好主管 大榮原則——人才是企業生存之本 ……第6章 創業定律 管他的，就去做吧 第7章 職場定律 到處都是有才華的失意人 第8章 兩性定律 理性選擇，感性相伴 ...
- 萊布尼茨函式
相伴的萊布尼茨標量函式，是從 到 的映射，把點M對應到數量 。設係數和 為零，那么函式可化簡成 其中 等於與這系統相伴的萊布尼茨向量函式的常值，是任意固定點。設係數和非零，那么函式可化簡成 其中 是系統 的重心。這個化簡令點的位置問題可以很容易解決（見萊布尼茨定理）。例：在2維情形，集 適合 的是 當...
- 第一類弗雷德霍姆積分方程
則稱只是特徵值，}S0}x) }杯x)是對應只的相伴特徵函式.施密特一皮卡定理斷言:設{只)和{SaCx)}},(x)}是方程(1>的所有特徵值和對應的規範正交相伴特徵函式對的系，又設規範正交系{}(x>}是完備的，則方程(1>有解的充分必要條件是級數藝}z}.f; I z c.f;一(cf,}>>)收斂;如果{}r}x)也是完備的...
- 配叢
配叢的一個相伴的概念是一個G-叢B的結構群的約化。我們問是否存在一個H-叢C，使得相配的G-叢是B（在同構的意義下）。更具體地，這是問B的轉移數據能否一致的取值於H中。換句話說，我們要求確認相配叢映射的像（這其實是一個函子）。約化的例子 向量叢的例子包括：引入一個度量導致結構群由一個一般線性群...
- 交換代數引論
2.2 Hilbert基定理 2.3 Hilbert零點定理 2.4 局部化 習題 第3章 代數集的分解與理想的準素分解 3.1 代數集的分解 3.2 理想的準素分解 3.3 相伴素理想 習題 第4章 維數 4.1 分次環與Hilbert多項式 4.2 代數集的維數 4.3 Noether環的維數 4.4 離散賦值環 習題 第5章 重複度與代數曲線的局部...
