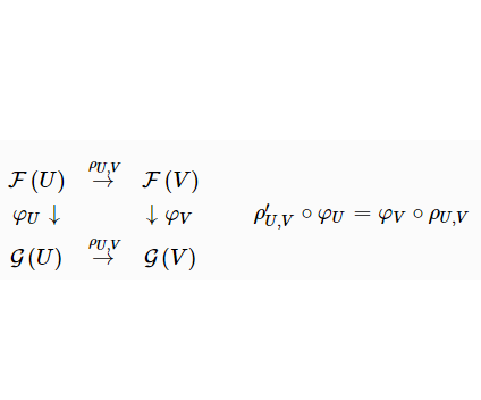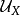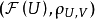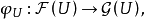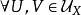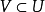層同態(sheaf homomorphism)是兩類之間的映射誘導出的一個群同態。設(F,π,X)與(F′,π′,X)是X上的兩個群層,若連續映射A:F→F′滿足π′A=π,且對所有x∈X,由A在莖上誘導出的映射Ax:Fx→Fx′是群同態,則稱A為一個層同態。若層同態A是同胚,且A-1也是層同態,則稱A為層同構。
基本介紹
- 中文名:層同態
- 外文名:sheaf homomorphism
- 所屬學科:數學
- 所屬問題:流形上的分析(層論)
定義,相關概念,層同構,層相伴空間的同態,層相伴空間的同構,相關定理,
定義
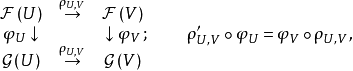

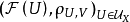

我們一般用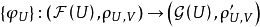 表示。
表示。
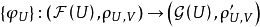
相關概念
層同構
設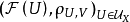 和
和 是拓撲空間X上兩個層,今有層同態:
是拓撲空間X上兩個層,今有層同態:
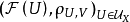






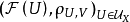

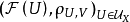

層相伴空間的同態
設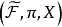 和
和 分別是拓撲空間X上的兩個層的相伴空間,
分別是拓撲空間X上的兩個層的相伴空間, 是一個連續映照,且適合
是一個連續映照,且適合
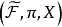


(1) 是保莖(preserves stalks)的,’即對
是保莖(preserves stalks)的,’即對 ,則
,則 ,對所有的
,對所有的 都成立。
都成立。




(2)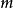 限制在莖上是群同態,即
限制在莖上是群同態,即
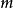

這樣的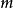 稱為層相伴空間
稱為層相伴空間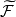 到層相伴空間
到層相伴空間 內的同態。
內的同態。
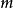
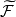

層相伴空間的同構
如果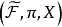 和
和 之假定同上,
之假定同上, 和
和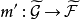 是兩個層相伴空間之間的同態,且有
是兩個層相伴空間之間的同態,且有 ,則稱
,則稱 是一個層相伴空間的同構,也說
是一個層相伴空間的同構,也說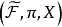 和
和 是同構的。
是同構的。
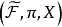


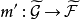


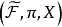

相關定理
定理1 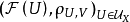 是拓撲空間X上的層,它與它的相伴空間的截影層
是拓撲空間X上的層,它與它的相伴空間的截影層 是同構的。
是同構的。
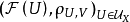

定理2設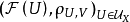 和
和 是拓撲空間X上的兩個層,
是拓撲空間X上的兩個層,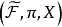 和
和 分別是它們的相伴空間,如果
分別是它們的相伴空間,如果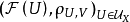 和
和 是層同構的,則相伴空間
是層同構的,則相伴空間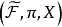 和
和 是同構的。
是同構的。
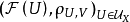

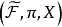

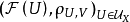

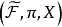

定理3設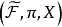 和
和 分別是拓撲空間X上的兩個層所對應的相伴空間,如果
分別是拓撲空間X上的兩個層所對應的相伴空間,如果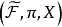 和
和 是相伴空間同構,則它們對應的截影層
是相伴空間同構,則它們對應的截影層 和
和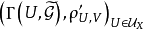 是層同構的。
是層同構的。
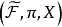

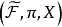


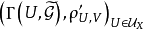
定理1、定理2和定理3說明了一個事實:即對—個拓撲空間X,它上面二個同構的層的相伴空間是同構的(定理2),反之,如果拓撲空間X上的二個層的相伴空間是同構的,則這二個層亦是同構的(因為由定理3知這二個相伴空間的截影層是同構的,而由定理1知每個截影層都同構於原來決定相伴空間的層,無疑層同構是一個等價關係,所以這二個層亦同構).因此我們可以將層和相伴空間看作是一樣的,由我們所討論的問題不同而作不同的選取。