直言三段論

直言三段論

直言三段論是所有前提都是直言命題的演繹推理。三段論是由包含著一個共同詞項的兩個直言命題（即：性質判斷）推出一個新的直言命題的推理。

基本介紹

定義,語氣和格,有效性,三段論剖析,

定義

直言三段論是所有前提都是直言命題的演繹推理。
例子：
  • 所有動物都會死。
  • 所有人都是動物。
  • 所以，所有人都會死。
前兩個命題叫做前提。如果這個三段論是有效的，這兩個前提邏輯上蘊含了最後的命題，它叫做結論。結論的真實性建立在前提的真實性和它們之間的聯繫之上：中項在前提中必須周延（distribute）至少一次，形成在結論中的主詞和謂詞之間的連線。即使直言三段論是有效的，但如果有前提為假的話結論仍可能是假。

語氣和格

三段論形式如下：
  • 大前提：所有M是P
  • 小前提：所有S是M
  • 結論：所有S是P
其中S代表結論的主詞（Subject），P代表結論的謂詞（Predicate），M代表中詞（Middle）。
三段論的命題可分為全稱（universal）、特稱（particular），及肯定、否定，組合起來有以下四類語氣（Mood）：
    類型代號形式範例
    全稱肯定型
    A（SaP）
    所有S是P
    所有人是會死的
    全稱否定型
    E（SeP）
    沒有S是P
    沒有人是完美的
    特稱肯定型
    I（SiP）
    有些S是P
    有些人是健康的
    特稱否定型
    O（SoP）
    有些S不是P
    有些人不是健康的
      三段論中，結論中的謂詞稱作大詞（P，或稱大項），包含大詞在內的前提稱作大前提；結論中的主詞稱作小詞（S，或稱小項），包含小詞在內的前提稱作小前提；沒有出現在結論，卻在兩個前提重複出現的稱作中詞（M，或稱中項）。大詞、中詞、小詞依不同排列方式，可分成四種格（Figure）：
        第1格第2格第3格第4格
        大前提
        M-P
        P-M
        M-P
        P-M
        小前提
        S-M
        S-M
        M-S
        M-S
        結論
        S-P
        S-P
        S-P
        S-P
          將以上整合在一起，三段論的大前提、小前提、結論分別可為A、E、I、O型命題之一，又可分為4格，故總共有256種三段論（若考慮大前提與小前提對調，便有512種，但邏輯上是相同的）。
          三段論依語氣與格的分類縮寫，例如AAA-1代表“大前提為A型，小前提為A型，結論為A型，第1格”的三段論。
          此外，三段論的四種格之間可相互轉換：
          • 第1格：不需轉換。
          • 第2格：對換大前提的前後兩項的位置就變成第1格，對換小前提的前後兩項的位置就變成第4格。
          • 第3格：對換大前提的前後兩項的位置就變成第4格，對換小前提的前後兩項的位置就變成第1格。
          • 第4格：對換大前提的前後兩項的位置就變成第3格，對換小前提的前後兩項的位置就變成第2格。
          E和I命題對換前後兩項的位置而保持同原命題等價。A命題不能對換前後兩項的位置，但可以在前項確實有元素存在的前提下，轉換成與弱於原命題的I命題。O命題不能對換前後兩項的位置。

          有效性

          考慮各種直言三段論的有效性將是非常冗長耗時的。幸運的是前人想出了三個可供選擇的方法來找出有效性。
          還可以通過構造文氏圖的方法得到有效形式。因為有三種項，文氏圖需要三個交疊的圓圈來表示每一個類。首先，為小項構造一個圓圈。臨近小項的圓圈的是同小項有著交疊的大項的圓圈。在這兩個圓圈之上是中項的圓圈。它應當在三個位置有著交疊：大項，小項和大項與小項交疊的地方。一個三段論是有效的，其必然條件是通過圖解兩個前提得出結論的真實性。永不圖解結論，因為結論必須從前提推導出來。總是首先圖解全稱命題。這是通過對一個類在另一個類中沒有成員的區域加黑影來實現的。所以在前面例子的AAA-1形式中大前提“所有M是P”中，對M不與P交疊的所有區域加黑影，包括M與S交疊的部分。接著對小前提重複同樣的過程。從這兩個前提中可推導出在類S中所有成員也是類P的成員。但是，不能推出類P的所有成員都是類S的成員。
          作為文氏圖方法的另一個例子，考慮形式EIO-1的三段論。它的大前提是“沒有M是P”，它的小前提是“有些S是M”，它的結論是“有些S不是P”。這個三段論的大項是P;它的小項是S，它的中項是M。大前提在圖中通過對交集M ∩ P加陰影表示。小前提不能通過對任何區域加黑影表示。轉而，我們可以在交集S ∩ M的非黑影部分使用x符號來表示“有些S是M”。（注意：黑影區域和存在量化區域是互斥的）。接著因為存在符號位於S內但在P外，所以結論“存在一些S不是P”是正確的。
          最後一種方法是記住下面非形式表述的幾條規則以避免謬論。儘管文氏圖對於詮釋目的是好工具，有人更喜歡用這些規則來檢驗有效性。
          基本規則：
          1. 結論中周延的詞必須在前提中周延（謬誤：大詞不當、小詞不當）
          2. 中詞必須周延至少一次（謬誤：中詞不周延）
          3. 結論中否定命題的數目必須和前提中否定命題的數目相等：
          4. 二前提皆肯定，則結論必須為肯定（謬誤：肯定前提推得否定結論）
          5. 一前提是否定，則結論必須為否定（謬誤：否定前提推得肯定結論）
          6. 二前提皆否定，則三段論必無效（謬誤：排它前提謬誤）
          其他檢查：
          • 如果語境上不能假設所有提及的集合非空，部分推論將會無效（謬誤：存在謬誤）
          • 必須包含嚴格的三個詞，不多不少。且須注意所有關鍵字和結構的語義是否一致（謬誤：四詞謬誤、歧義謬誤）

          三段論剖析

          三段論在結構上包括大項、中項和小項。大項是作為結論的謂項的概念，小項是作為結論的主項的概念，中項是在前提中出現兩次而在結論中不出現的概念。
          三段論的兩個前提分別叫做大前提和小前提。其中，包含大項的叫大前提，包含小項的叫小前提。按照通常的習慣，大前提在前面，小前提在後面。但是，排列的順序不是區分大、小前提的標準。區分大、小前提，只能看它們是包含大項還是包含小項。中項在三段論中十分重要，它起到把大、小前提連線起來，從而推出結論的橋樑和紐帶作用。
          在三段論中，大項通常用P表示，小項用S表示，中項用M表示。這樣，上述推理的一般公式可以表示為：
          所有的M都是P。
          所有的S都是M。
          → 所有的S都是P。
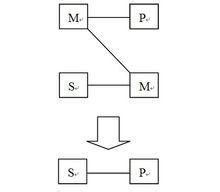          圖1.直言三段論的說明圖圖1.直言三段論的說明圖
          三段論的判定規則
          一個三段論是否正確，可以通過下面規則來加以判定。
          有且只有三個不同詞項
          違反這條規則，通常出現的錯誤成為“四詞項”或“四概念”。
          中項至少周延一次
          中項要起到媒介作用，必須至少有一部分外延既與大項建立關係，又與小項建立關係。如果中項至少周延一次，那么，中項的全部外延就與大項或小項建立了聯繫，這樣就能確保至少有一部分外延同大小項存在關係。違反這條規則，就要犯“中項兩次不周延”的邏輯錯誤。
          例如：
          壞人都攻擊我。
          你攻擊我。
          → 你是壞人。
          上例中的中項“攻擊我”，在前提中兩次都是肯定命題的謂項，都不周延，犯了“中項兩次不周延”的邏輯錯誤。
          前提中不周延的詞項結論中也不能周延
          這條規則是對大項和小項的外延的規定。三段論是一種必然性的推理，它要求，不能從部分推出全部，不能從不周延的詞項過渡到周延的詞項，否則推理就不具有必然性了。違反這條規則，就犯了“大項不當周延”或者“小項不當周延”的邏輯錯誤。
          “大項不當周延”是指大項在前提中不周延，而在結論中變得周延了
          兩個否定前提推不出結論
          如果三段論的兩個前提都是否定的，那么小項和大項必然都同中項相排斥，這樣，中項就無法起到連線大小項的作用，作不出形式有效的推導。
          如果前提中有一個否定，那么結論就是否定的
          如果前提中有一個是否定的，那么小項和大項之一必然同中項排斥，無論是小項同中項相排斥，還是大項同中項相排斥，在結論中小相同大項必然相排斥，結論必然是否定的。

          相關詞條

          熱門詞條

          聯絡我們