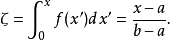直接抽樣法

直接抽樣法是對於任意給定的分布函式F(x)，產生其樣本的一種抽樣方法。

基本介紹

• 中文名：直接抽樣法
• 外文名：direct sampling technique
• 作用：產生樣本
• 套用領域：數學
• 套用類型：離散型和連續型的隨機變數

概念

直接抽樣法是一種常用的方法，對連續型和離散型的隨機變數均有效。對於連續型隨機變數，套用該法必須求得該分布函式的反函式。另外，對於離散型分布，直接抽樣方法的優點是簡單明了，易於實現，缺點是當離散點數多時，抽樣速度慢。對於連續型分布，當容易計算，而且運算量又不大時，直接抽樣方法是最理想的方法。不過，在實際問題中具有這樣性質的情況很少。

原理

設y=F(x)為隨機變數x的累積分布函式，即x和y是一一對應的，先隨機抽取y，然後通過求F(x)的反函式 得到隨機變數x的值

隨機變數y在[0,1]區間上均勻分布，利用[0,1]區間上均勻分布隨機數產生器抽取，即可得到樣本。

方法

U[0,1]:[0,1]區間上均勻分布的隨機數的抽樣步驟：

1. 從U[0,1]抽取隨機數ζ；
2. 令F(x)=ζ；
3. 解方程得x

註：需要知道累積分布函式的解析表達式，且累積分布函式的反函式存在。

不同函式抽樣

分離型隨機變數的抽樣

直接抽樣法適應於分離型的隨機變數

方法

1. 計算

2.從U[0,1]抽取隨機數ζ；

3.求滿足 的K值；

4.隨機變數的第k個取值即為欲抽取的值。

粒子衰減末態的隨機抽樣

設粒子a有三種衰變方式，其分支比如表1所示：

表1 粒子的衰變方式

a→	b1+c1	p1=0.5
	b2+c2	p2=0.3
	b3+c3	p3=0.2

方法

隨機選取每次衰變的衰變方式（衰變道），ζ∈U[0,1]，如表2所示：

表2 隨機選取的衰變方式

0〈ζ〈0.5	b1+c1
0.5〈ζ〈0.5+0.3	b2+c2
0.5+0.3〈ζ〈1	b3+c3

區間上均勻分布的隨機數

方法：

產生ζ∈U[0,1]；

指數分布

方法：

產生ζ∈U[0,1]；