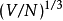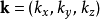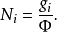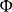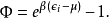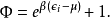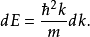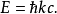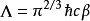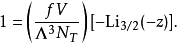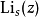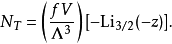基本介紹
- 中文名:盒中氣體
- 外文名:Gas in the box
- 定義:不會互相作用的粒子
- 相關術語:費米氣體、玻色氣體
- 學科:量子力學
- 領域:量子力學
量子數極大近似,能量分布函式,正質量粒子,零質量粒子,範例,相關條目,
量子數極大近似
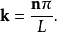
粒子的每一個可能的量子態,可以想像為處於一個三維k-空間的一點,坐標是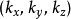 。每一點離最近鄰點的距離是
。每一點離最近鄰點的距離是 。在這三維k-空間內,每一個量子態占據了
。在這三維k-空間內,每一個量子態占據了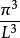 的k-空間。從k-空間的原點到k的距離是
的k-空間。從k-空間的原點到k的距離是
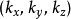

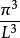
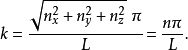
假設f是每種粒子內涵的自由度。當粒子遇到碰撞時,f是粒子可以被改變的自由度。那么,每一組量子數設定了f個量子態。這f個量子態占據了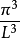 的k-空間。例如,一個自旋為1/2的粒子,有兩個自旋態,自由度為f=2。
的k-空間。例如,一個自旋為1/2的粒子,有兩個自旋態,自由度為f=2。
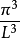
假定系統的量子數極大,則可以將量子數視為連續值。那么,波數小於或等於k的量子態的數量大約為

這只是f乘以一個半徑為k的圓球容積的八分之一的乘積。請注意這裡只有用到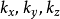 為正值的圓球部分,k-圓球的八分之一。所以,波數在k與k+dk之間的量子態的數量大約為
為正值的圓球部分,k-圓球的八分之一。所以,波數在k與k+dk之間的量子態的數量大約為
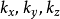

注意到在使用這連續近似的同時,我們也失去了計算低能量量子態特性的能力,包括基態n=1。對於大多數的案例,這不是問題。可是,當思考像玻色-愛因斯坦凝聚這類的問題時,由於大部分的氣體處於基態或其鄰近量子態,低能量量子態的影響變得很重要。
不使用連續近似,能量為 的粒子的數量
的粒子的數量 為
為


使用連續近似,波數在k與 k+dk之間的粒子的數量dN為

能量分布函式
有了前面幾段導引出來的結果,我們現在可以開始計算盒子氣體的某些分布函式。
粒子的A值在A與A+dA之間的機率是
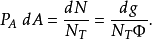
這表達式的積分是總機率,等於1:

按照這些公式,波數的分布函式可以表達為

能量E的分布函式是

計算 以前,必須先知道波數與能量的關係方程。
以前,必須先知道波數與能量的關係方程。

正質量粒子
對於正質量粒子,
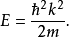
將E與dE的公式代入公式(2),再稍加運算,可得到
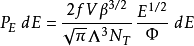
其中, 是正質量粒子的熱波長或熱德布羅意波長(thermal de Broglie wavelength)。
是正質量粒子的熱波長或熱德布羅意波長(thermal de Broglie wavelength)。

熱波長是一個很重要的物理量。當熱波長接近粒子與粒子之間距離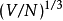 時候,量子效應開始成為主導機制,氣體不能被視為麥克斯韋-玻茲曼氣體。
時候,量子效應開始成為主導機制,氣體不能被視為麥克斯韋-玻茲曼氣體。