多重對數(polylogarithm)是一種特殊函式。與對數函式不同,多重對數並非初等函式。由這個定義,其定義域為{z| |z|<1},即所有模小於一的複數的集合。但我們還可以通過解析開拓(analytic continuation)將其定義域拓展至一個更大的區域。
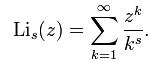 多重對數定義
多重對數定義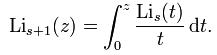 多重對數用積分定義
多重對數用積分定義 實部
實部 虛部
虛部多重對數(polylogarithm)是一種特殊函式。與對數函式不同,多重對數並非初等函式。由這個定義,其定義域為{z| |z|<1},即所有模小於一的複數的集合。但我們還可以通過解析開拓(analytic continuation)將其定義域拓展至一個更大的區域。
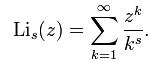 多重對數定義
多重對數定義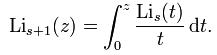 多重對數用積分定義
多重對數用積分定義 實部
實部 虛部
虛部多重對數(polylogarithm)是一種特殊函式。與對數函式不同,多重對數並非初等函式。由這個定義,其定義域為{z| |z|<1},即所有模小於一的複數的集合。但我們還...
多重對數函式(polylogarithm)是一種特殊函式,通俗地講,就是使得log(i) * n ≦ 1 的最小i值。...
多重對數函式,當勒奇函式中a=1,則化為多重對數函式 勒奇超越函式積分形式 編輯 勒奇超越函式級數展開 編輯 參考資料 1. Erdélyi A. Higher Transcendental ...
其中, 是多重對數(polylogarithm)。所以,總粒子數為盒中氣體相關條目 編輯 費米氣體 黑體輻射 白矮星 中子星 全同粒子 參考資料 1. Huang, Kerson. ...
(對頻率的玻色積分項的計算方法參見條目多重對數函式) [1] 斯特藩-玻爾茲曼定律日面溫度 編輯 提出本定律後斯特藩利用它估算了太陽的表面溫度。當時法國人查理·...
其中對於 和s>1成立,其中 代表多重對數。赫爾維茨ζ函式泰勒展開 編輯 赫爾維茨ζ函式的導數是平移:因此赫爾維茨ζ函式的泰勒級數可表示為:...
是m階多重對數。狄拜方程式漸近式 對於 對於 :圖1 德拜函式 狄拜方程式相關函式 編輯 也有將德拜函式定義為:狄拜方程式相關理論 編輯 狄拜...
是m階多重對數。 [2] 德拜函式漸近式 對於 對於 : [3] 圖1 德拜函式 德拜函式相關函式 編輯 也有將德拜函式定義為:參考資料 1. Gradshteyn I S, Ryzhi...
