基本介紹
- 中文名：費米氣體
- 外文名：Fermi gas
- 別稱：自由電子氣體
- 屬性：量子統計力學
- 統計規律：費米-狄拉克統計，非廣延統計
簡介,統計性質,理想費米氣體,弱相互作用費米氣體,強相互作用費米氣體,統計規律,研究回顧,
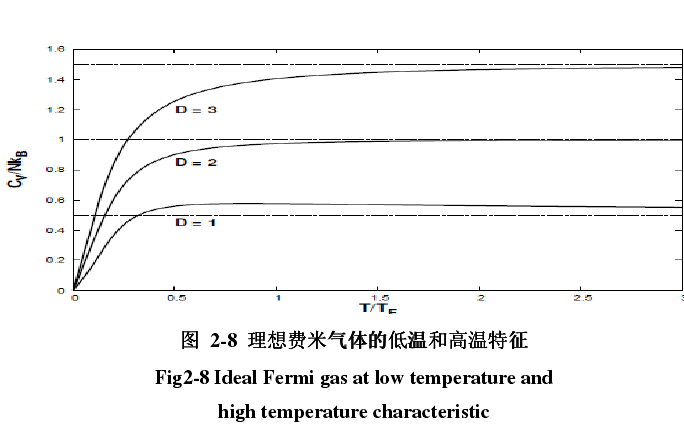
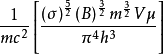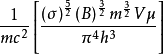簡介
費米氣體是借用理想氣體模型描述費米子系統性質的量子力學模型。該模型中，粒子所處的量子態可用它們具有的動量來表征。對於周期性系統，譬如在金屬原子點陣中運動的電子，亦可類似地引入“準動量”的概念以表征量子態（參見條目布洛赫波）。無論上述哪種模型，其具有費米能的量子態都處於動量空間中的一個確定的曲面上，這個曲面稱為費米面。費米氣體的費米面是一個球面；周期體系中的費米面則通常是扭曲面。費米面包圍的體積決定了系統中的電子數，而費米面的拓撲結構則與金屬的各種傳導性質（如電導率）直接相關。對費米面的研究有時被稱為“費米學”（Fermiology）。如今，絕大多數金屬的費米面均已經有較透徹的理論與實驗研究。
統計性質
費米氣體模型：理想費米氣體，弱相互作用費米氣體，強相互作用費米氣體
理想費米氣體
D維空間理想費米氣體的統計性質
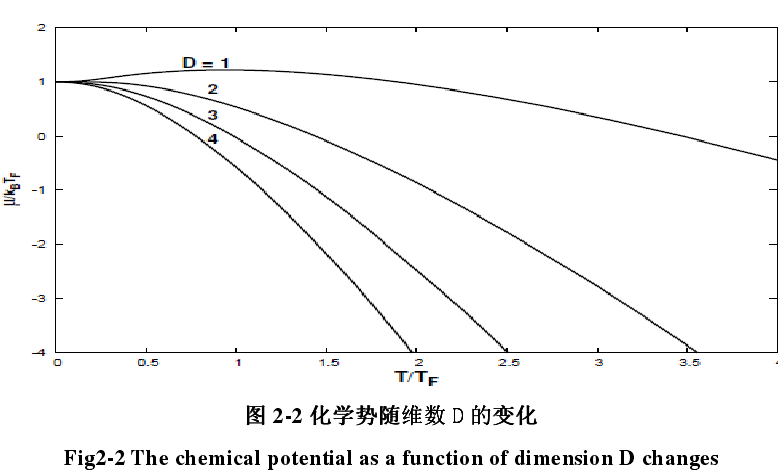
下面圖中給出了化學勢與溫度之間的關係，從圖中可以看出化學勢隨著溫度的增大而降低，當維數不同時化學勢的下降情況也是不同的。圖示為能級隨維數的變化，從圖中可以看出D越大變化越慢。
理想費米氣體的低溫特徵和高溫特徵。
q-費米氣體的統計性質
當q<1 和µ>0時，費米子的能量不應比化學勢大。在零溫時費米能級EF下的所有能級都被費米子，而費米能級EF上的所有能級都是空的。
當 q≠1 時費米體系的化學勢不僅依賴於溫度而且依賴於參數q 和δ。當q>1時，費米體系的化學勢小於費米能。當 q<1時，費米體系的化學勢大於費米能。當q<1相同時費米體系的熱容量隨q 而增加但不是溫度的單調函式。當q>1時， 費米體系的熱容量隨溫度單調增加。當 q<1時，費米體系的熱容量趨於零。當 q=1 時費米體系的熱容量是溫度的單調函式。
弱相互作用費米氣體
（1）無論在低溫還是高溫條件下，磁場總是引起費米體系的能量的減小和化學勢的增加，在高溫下熱容量增加而在低溫下熱容量減小，還減小了系統的穩定性。在高溫下磁場對熱力學量的影響與溫度有關，溫度越高影響越弱。在低溫下磁場對能量和化學勢的影響與溫度有很小的相關性。磁場對能量和熱容量的影響與總粒子數成正比，但磁場對化學勢的影響與總粒子數無關。
（2）吸引（排斥）作用總是增加（減小）費米體系的能量，減小（增加）費米體系的順磁性，在高溫下相互作用對順磁性的影響與溫度有關，溫度越高影響越弱。在低溫下相互作用對順磁性的影響與溫度無關，但與費米溫度有關。吸引（排斥）作用總是增加（減小）費米體系的化學勢，在高溫下排斥（吸引）作用通過磁場減小（增加）費米體系的熱容量，在低溫下排斥（吸引）作用不會通過磁場增加（減小）費米體系的熱容量。粒子間的相互作用不僅直接而影響熱力學性質，也會調節磁場對熱力學性質的影響，排斥（吸引）作用總是通過磁場增加（減小）對費米體系化學勢的影響。排斥（吸引）作用總是增加（減小）對費米體系的穩定性。同時考慮自旋和軌道運動，在高、低溫條件下相互作用對熱容量的影響相反。
強相互作用費米氣體
低溫性質
只要T≠0，磁場對費米氣體統計性質的影響包含諧振和非諧振兩個部分，對於非諧振部分，與弱磁場中的費米氣體相比較，磁場對化學勢、費米能和穩定條件的影響發生了改變。對諧振部分，磁場影響了諧振的周期和振幅。諧振周期很小並且正比於σB/εF，在T~σB條件下，諧振的振幅正比與因子σB/εF。費米體系的基態能和費米能沒有諧振，與自由費米氣體相比較，磁場總是降低費米體系基態能和費米能，當T≠0時，由於化學勢有諧振，在特殊的磁場和溫度條件下，費米體系的化學勢也許比費米能大。
從費米體系熱力學量的的分析中可以看出，與非諧振部分相比較，費米體系的總能量比較小，熱容量比較大，而化學勢則相同。在T~σB和σB/εF<< 1條件下，即使有震盪部分，費米體系也能保持熱力學穩定性。
相對論效應
相對論效應對能量、化學勢、平均磁矩的影響仍然分為兩部分，即隨磁場變化的振盪部分與單調（非振盪）部分.由於µ≫σB ,從隨磁場變化的單調部分來看，相對論效應使總能、化學勢降低，而使磁矩增加。其量值分別比例於：
、
、
。顯然這些量值都與磁場B成正比，而且也與粒子數密度n有關.相對論效應對熱容量的影響僅有振盪部分，在T∼σB 的條件下，其振幅比例於
。
在考慮相對論效應所產生的振盪項中，振盪的頻率或周期仍然與非相對論情況相同，只是振盪的相位比非相對論情況落後了π/2。在T∼σB 的強磁場條件下，總能、化學勢、磁矩的振幅分別比例於：
、
、
；相應的振幅與單調部分的比值分別為：
、
、 。由此表明，考慮相對論效應所引發的單調項與振盪項的振幅二者相比較，對於總能，單調項遠大于振幅；對化學勢和磁矩而言，單調項與相應的振幅幾乎同一量級，且二者的比值與磁場、溫度無關。
統計規律
費米氣體的統計規律有：費米-狄拉克統計，非廣延統計。
費米氣體是理想氣體的量子力學版。在金屬內的電子、在半導體內的電子、或在中子星里的中子，都可以被視為近似於費米氣體。在一個處於熱力平衡的費米氣體裡，費米子的能量分布，是由它們的密度，溫度，與容許能量量子態集合，依照費米-狄拉克分布方程而決定的。泡利不相容原理闡明，不容許被兩個或以上的費米子占用同一個量子態。因此，在絕對零度，費米氣體的總能量，大於費米子數量與單獨粒子基態能量的乘積。並且，在絕對零度，費米氣體的壓力，稱為“簡併壓力”，不等於零。這與經典理想氣體的現象有很明顯的不同。簡併壓力使得中子星或白矮星能夠抵抗萬有引力的壓縮，因而得到穩定平衡，不致向內爆塌。
在低溫下，玻色原子氣體可以形成玻色-愛因斯坦凝聚(Bose-Einstein condensation, BEC)，這是由Einstein在1925年的理論而預言的。費米子由於泡利不相容原理，不能形成BEC。但可通過Feshbach共振，利用磁場調節費米原子間的相互作用，使費米子配對轉變成玻色型粒子而形成BEC。
由於前述定義忽略了粒子與粒子之間的相互作用，費米氣體問題約化為研究一群獨立的費米子的物理行為的問題。這問題本身相當容易解析。一些更深奧，更進階，更精密的理論，牽涉到粒子與粒子之間的互相作用的理論（像費米液體理論或相互作用的微擾理論），時常會以費米氣體問題為研究的開端。
研究回顧
關於量子氣體的研究最早可追溯到 20 世紀20 年代。1926 年6 月24 日，印度S.Bose用英文寫了題為《Plank 準則和光量子假設》的論文，認為熱輻射是全同的光子氣體，並服從於Bose -Einstein 統計理論推導出Plank 熱輻射光譜分布黑體輻射公式。7 月又寄給 A.Einstein.，Einstein 認識到其重要性，將Bose 的方法推廣到單原子理想氣體，認為當理想氣體溫度很低時會凍結在儘可能低的系統能級上。次年又指出當原子的 deBroglie 熱波長大於原子間的平均距離時，才會出現凝聚。而在 1926 年初, 費米在《關於單原子理想氣體的最子化》中首先在舊量子論的框架提出了 Fermi-Dirac 統計理論。這篇論文先在義大利發表,後被他譯成德文，寄給當時物理學方面權威性的雜誌—德國《物理期刊》，同年 3月26 日收到並發表。同年8 月，狄拉克《關於量子力學理論》在英國皇家學會刊物上刊出。在這篇論文中, 狄拉克接受波動力學新理論，把握住量子統計的核心——體系波函式的對稱性，也獨立地提出了 Fermi-Dirac 統計理論。按照另一種說法，約當 1925 年建立了同樣的統計，只是稱之為泡利統計，但是並沒有發表。然而狄拉克認為這首先由費米發現，因而稱之為費米統計，相應的粒子稱為費米子。1926年，福勒首先用費米-狄拉克統計描述星體塌縮為白矮星。1927 年索末菲把它套用於金屬中的電子，1928 年福勒和Nordheim 把它套用於金屬中的場電子發射。因而費米-狄拉克統計成為物理學中的重要部分。20 世紀50 年代之前，量子統計（Quantum Statistical）一般處理無相互作用的量子氣體，即理想費米和玻色氣體。由於理論上和數學上的困難，還不能處理有相互作用的實際體系。
五十年代開始，由基本粒子研究而發展起來的量子場論逐步成熟，量子場論方法（有效平均場理論、微擾論、變分法、密度泛函理論、費曼圖、格林函式方法、路徑積分方法、重整化群、共形場論等）開始進入量子統計領域，在若干基本理論問題中解決了多個有實際意義的難題，從此，量子統計理論得到迅速的發展，很快成為理論物理中的重要分支，並為量子體系基本理論的研究提供了有效的理論方法和實際的檢驗場所。
