基本介紹
- 中文名：球面小圓
- 外文名：spherical small circle
- 所屬學科：數學
- 所屬問題：立體幾何（球面幾何）
- 簡稱：小圓
- 簡介：平面不通過球心時與球面相交的圓
基本介紹,例題解析,
基本介紹
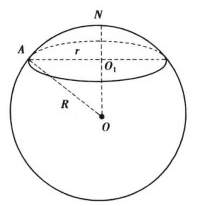圖1球面圓是球面幾何的基本概念之一，是球面在空間中與平面相交時的交線圓，包括平面通過球心時交成的球面大圓和平面不通過球心時與球面相交而成的球面小圓。垂直於球面圓所在平面的直徑的兩個端點(對徑點)稱為球面圓的球面中心，亦稱為球面圓的極。球面大圓的圓弧、優弧、劣弧、余弧、共軛弧依次稱為球面大圓弧、大圓優弧、大圓劣弧、余大圓弧、共軛大圓弧。當提到連結球面上非對徑的兩點的大圓弧時，通常指大圓劣弧，此大圓弧的長度稱為此兩點間的球面距離。因為球面上非對徑的兩點與球心不共線而決定一個平面，這兩點就在由此平面與球面相交的惟一大圓上，所以上述球面距離的定義適用於球面上非對徑的任意兩點，至於球面的兩個對徑點，自然地以半大圓弧的長度作為它們的球面距離，球面圓的球面中心與球面圓上的點的球面距離相等，即球面圓是球面上與一個定點的距離等於定值的點的軌跡，此定點即球面圓的球面中心或極，這個定值稱為球面圓的球面半徑，亦稱為球面圓的角半徑、弧半徑或極距，球面大圓的球面半徑等於一象限弧，球面小圓與兩個球面中心(極)相應有小於和大於一象限弧的兩個球面半徑，球面半徑小於一象限弧的極稱為近極，另一個稱為遠極，由於球面小圓的球面中心通常是指離該圓所在平面的距離較近的那個近極，因此，球面小圓的球面半徑通常指小於一象限弧的那一個。在空間直角坐標系中，球心為點(a，b，c)半徑為R的球面的方程是
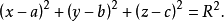
例題解析
【例1】球面上有三個點，其中任意兩個點的球面距離都等於大圓周長的1/6，經過這三個點的小圓周長為4π，那么這個球的半徑為( )。
A.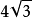
B.
C.2 D.3
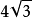
分析 設該球球心為O，半徑為R，球面上三點為A，B，C，則依據題意知O-ABC是正三稜錐，側棱長即為球的半徑R。
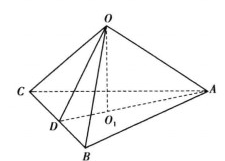圖2如圖2，由已知得，兩條側棱的夾角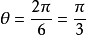
，正三角形ABC外接圓半徑
。在三角形ABC中，由正弦定理得:AB=2r sin 60°=。故選B。
【例2】如圖3，A,B,C是表面積為48π的球面上三點，AB =2,BC =4,∠ABC =60°，O為球心，則直線OA與截面ABC所成的角是( )。
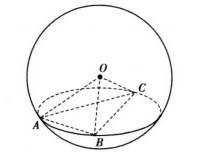圖3