基本介紹
- 中文名:玻恩-奧本海默近似
- 外文名:Born-Oppenheimer approximation
- 別稱:定核近似或絕熱近似
- 適用性:電子態能量都足夠分離
簡介
適用性
最低值原理
凝聚態物理學
相關條目
- 玻恩-黃近似
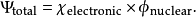
玻恩–奧本海默近似(Born-Oppenheimer approximation,簡稱BO近似,又稱絕熱近似)是一種普遍使用的解包含電子與原子核的體系的量子力學方程的近似方法。...
玻恩–奧本海默近似(Born-Oppenheimer approximation,簡稱BO近似,又稱絕熱近似)是一種普遍使用的解包含電子與原子核的體系的量子力學方程的近似方法。...
在量子力學中,玻恩-黃近似是求解分子體系薛丁格方稱的一種近似方法。這個由提出者馬克斯·玻恩與黃昆命名的方法[1] 與玻恩-奧本海默近似緊密關聯且十分相似。這兩...
1. 以他名字命名的玻恩-奧本海默近似方法在1928年發展成為原子軌道模型,玻恩近似在分布理論中起到了先驅作用。2. 以馬克斯·玻恩的名字命名的研究所——柏林馬克斯...
玻恩–奧本海默近似(Born-Oppenheimer approximation,簡稱BO近似,又稱絕熱近似)是一種普遍使用的解包含電子與原子核的體系的量子力學方程的近似方法。...
而認為電子分子哈密頓的本徵函式隨分子幾何形狀緩慢變化的想法則被稱為波恩-奧本海默近似。 近似的粗略推導(不精確, 但定性正確) 原子核的質量遠大於環繞它們的...
英文名稱:adiabatic photoreaction在玻恩-奧本海默近似條件下,在單個勢能面上激發態物種的反應。...
diabatic photoreaction 在玻恩-奧本海默近似下,一個反應開始於一種激發態的勢能面上,通過無輻射躍遷終止在另一勢能面上時,稱為非絕熱光反應。後一狀態通常為基態...
在玻恩-奧本海默近似下對原子核坐標變數與電子變數進行分離後,與核自由度相關的波包通過與含時薛丁格方程全哈密頓量相關的演化算符進行傳播。而在以能量本徵態為...
建立在玻恩-奧本海默近似上的雙原子分子電子態理論中,的問題占有重要地位。它的玻恩-奧本海默態可以嚴格求解,結果與實驗符合很好。MO-LCAO近似,即假定分子軌道(MO)...
在玻恩-奧本海默近似條件下,一個多電子體系的電子運動與能量可以與原子核的運動和能量相互分離,這樣利用電子哈密頓算符和多電子波函式便可以計算體系的電子能量。其...
在研究多原子分子電子態時,一般也是採用玻恩-奧本海默近似(見雙原子分子電子態),即把分子中電子運動和分子的振動、轉動分開。由分子中的電子按最低能量狀態填充時...
2、提出了量子絕熱近似高階修正方法和推廣的玻恩-奧本海默近似,發現了誘導規範場的可觀測效應。基於量子比特絕熱操縱,研究了固態量子比特的相干集成、納米機械冷卻和...
10.5.5偶極近似和振子強度10.5.6氫原子的躍遷機率和振子強度表習題第11章原子分子等的近似處理11.1電子運動與核運動的近似分離11.1.1玻恩奧本海默近似...
米格達爾定理實質上是玻恩-奧本海默近似。所以強耦合超導理論的精確度是(m/M),這裡m是電子的質量,M是原子的質量。對於鋁,這個比值大約是百分之零點五,對於鉛和...
非玻恩-奧本海默近似問題超冷原子晶片中子星高能輻射的觀測研究宇宙中的中微子宇宙學起源的引力波研究宇宙弦的演化參考資料 1. 10000個科學難題·物理學卷 ..[引用...
後者是求解薛丁格方程的經典方法,以計算一個分子的基態性質為例,科學家首先要將薛丁格方程作玻恩-奧本海默近似、單電子近似、HF平均場近似和原子軌道線性疊加等處理,...
取消原子核的動能算符而算得以核構形中各原子核坐標為參數的電子波函式,這就是玻恩-奧本海默近似。在初步近似中,可用單電子波函式來描述各電子的狀態。電子的...
後者是求解薛丁格方程的經典方法以計算一個分子的基態性質為例,科學家首先要將薛丁格方程作玻恩-奧本海默近似,單電子近似,HF平均場近似和原子軌道線性疊加等處理,化...
