基本介紹
- 中文名:狄利克雷定理
- 外文名:Dirichlet's theorem on arithmetic progressions
- 提出者:狄利克雷
- 套用學科:數學
- 適用領域範圍:物理
- 推廣定理:Chebotarev密度定理
人物介紹
定理定義

驗證推導



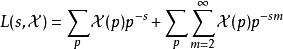





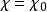




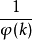





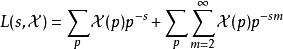





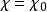




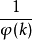
在數論中,狄利克雷定理說明對於任意互質的正整數a,d,有無限多個質數的形式如a+nd,其中n為正整數,即在等差數列a+d,a+2d,a+3d,...中有無限多個質數——...
狄利克雷單位定理是代數數論中描述任意代數數域K中單位群結構的基本定理,最早由德國數學家狄利克雷給出。...
約翰·彼得·古斯塔夫·勒熱納·狄利克雷(Johann Peter Gustav Lejeune Dirichlet),德國數學家。科隆大學博士。歷任柏林大學和格廷根大學教授。柏林科學院院士。是解析...
約翰·彼得·古斯塔夫·勒熱納·狄利克雷(Johann Peter Gustav Lejeune Dirichlet,勒熱納·狄利克雷是姓,1805年2月13日-1859年5月5日),德國數學家。他是解析數論...
狄利克雷L函式,又稱對應於模q的特徵Ⅹ(n)的狄利克雷L函式。...... 約翰·彼得·狄利克雷證明對所有 χ 俱有L (1,X)≠0,並藉此證明狄利克雷定理。若χ ...
歐幾里得定理是數論中的基本定理,定理指出素數的個數是無限的。該定理有許多著名...歐幾里得定理參閱 編輯 狄利克雷定理 素數定理 參考資料 1. 朱文杰, 易本順, ...
數學定理列表(按字母順序排列) 以下列出了許多數學定理,供查閱與引用。...迪尼定理等周定理代數基本定理多項式餘數定理大數定律狄利克雷定理...
諾伊曼從事狄利克雷定理,可以被認為是積分方程理論的發起者之一。諾伊曼級數,類似於幾何級數:對無限矩陣的條件下的原理是以他命名而來的。...
,a+nd,…(1)中,當a與d為互素的正整數時,必有無窮多個素數.這就是著名的狄利克雷定理,是德國數學家狄利克雷(Dirichlet,P. G. L.)於1837年發表的重要...
乘性數論藉由研究積性生成函式的性質來探討素數分布的問題,其中質數定理與狄利克雷定理為這個領域中最著名的古典成果。加性數論則是研究整數的加法分解之可能性與...
積性數論藉由研究積性生成函式的性質來探討質數分布的問題,其中質數定理與狄利克雷定理為這個領域中最著名的古典成果。加性數論則是研究整數的加法分解之可能性與...
它首次出現在數學家狄利克雷在1837年導入狄利克雷L函式,來證明狄利克雷定理。解析數論的成果中,較廣為人知的是在質數(例如質數定理及黎曼ζ函式)及堆疊數論(例如...
α=0的特殊情況稱為狄利克雷定理。矩陣的Kronecker乘法對n×m階矩陣A和p×q階矩陣B,A和B的Kronecher乘法運算可定義為:注意:右圖中A為m*n維矩陣...
