牛頓多邊形(Newton's polygon)是一階亨澤爾域上多項式可約性的一種判別法。亨澤爾域亦稱亨澤爾賦值域。一種重要的賦值域。若φ是域F的一個亨澤爾賦值,則稱賦值域(F,φ)為亨澤爾域,或稱亨澤爾賦值域。
基本介紹
- 中文名:牛頓多邊形
- 外文名:Newton's polygon
- 領域:數學
- 性質:可約性判別法
- 對象:亨澤爾域上多項式
- 人物:牛頓
概念

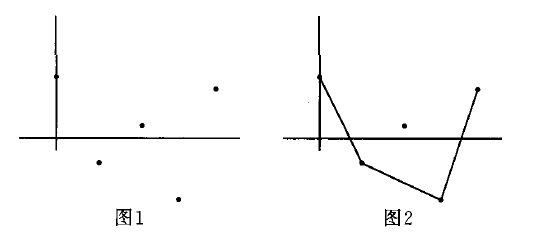
牛頓多邊形(Newton's polygon)是一階亨澤爾域上多項式可約性的一種判別法。亨澤爾域亦稱亨澤爾賦值域。一種重要的賦值域。若φ是域F的一個亨澤爾賦值,則稱賦值域(F,φ)為亨澤爾域,或稱亨澤爾賦值域。


牛頓多邊形(Newton's polygon)是一階亨澤爾域上多項式可約性的一種判別法。亨澤爾域亦稱亨澤爾賦值域。一種重要的賦值域。若φ是域F的一個亨澤爾賦值,則稱賦值域(F,φ)為亨澤爾域,或稱亨澤爾賦值域。概念牛頓多...
多邊形內角和定理證明 證法一:在n邊形內任取一點O,連結O與各個頂點,把n邊形分成n個三角形.因為這n個三角形的內角的和等於n·180°,以O為公共頂點的n個角的和是360° 所以n邊形的內角和是n·180°-2×180°=(n-2)·180°.(n為邊數)即n邊形的內角和等於(n-2)×180°.(n為邊數)證法...
《牛頓書院:國中數學基礎知識手冊》是2012年雲南教育出版社出版的圖書,作者是劉高峰、張天悅。內容簡介 《牛頓書院:國中數學基礎知識手冊》由一線名師權威打造,是莘莘學子備考寶典,薈萃知識精華,掌握中考考點。內容全面,品質精良,它緊扣考試大綱,知識講解層次鮮明,題型全面,題量適中,思想方法總結齊全,規律技巧點撥...
正多邊形是指二維平面內各邊相等,各角也相等的多邊形,也叫正多角形。定義 各邊相等,各角也相等的多邊形叫做正多邊形。正多邊形的外接圓的圓心叫做正多邊形的中心。正多邊形的外接圓的半徑叫做正多邊形的半徑。中心到圓內接正多邊形各邊的距離叫做邊心距。正多邊形各邊所對的外接圓的圓心角都相等,這個圓心角叫做正多邊形...
凸多邊形是一個內部為凸集的簡單多邊形。凸多邊形(Convex Polygon)指如果把一個多邊形的所有邊中,任意一條邊向兩方無限延長成為一直線時,其他各邊都在此直線的同旁,那么這個多邊形就叫做凸多邊形,其內角全不是優角,任意兩個頂點間的線段位於多邊形的內部或邊上。定義 凸多邊形(Convex Polygon)可以有以下三種...
牛頓疊代法(Newton's method)又稱為牛頓-拉夫遜(拉弗森)方法(Newton-Raphson method),它是牛頓在17世紀提出的一種在實數域和複數域上近似求解方程的方法。產生背景 多數方程不存在求根公式,因此求精確根非常困難,甚至不可解,從而尋找方程的近似根就顯得特別重要。方法使用函式 的泰勒級數的前面幾項來尋找...
對於n次多項式F(X)有著名的牛頓恆等式。它是n次方程F(X)=0的n個根的同次冪的和與F(X)的函式之間關係的明確表述。背景 艾薩克·牛頓(Isaac Newton)是英國偉大的數學家、物理學家、天文學家和自然哲學家,其研究領域包括了物理學、數學、天文學、神學、自然哲學和鍊金術。牛頓的主要貢獻有發明了微積分,發現...
《數論中的p-adic方法》是依託四川大學,由洪紹方擔任項目負責人的面上項目。項目摘要 利用Dwork的p-adic理論和方法,特別地利用Dwork跡公式,研究三維扭曲Kloosterman和的L函式的p-adic牛頓多邊形,研究一元和二元多項式的扭曲指數和的L函式的p-adic牛頓多邊形及其漸近行為,特別地,研究低次數多項式的扭曲指數和L函式的p-...
蘊含了重要的算術與幾何信息. 代數簇中多項式(組)的次數在指數和的估計及L-函式的p-adic牛頓多邊形中占據著重要地位, 但已有文獻中關於次數變動特別是降次對後二者的影響並不多見. 本項目的主要研究對象是有限域上代數簇的指數和及其L-函式,重點研究降次對指數和估計及其L-函式的p-adic牛頓多邊形的影響。
A.4.1.冪級數的牛頓多邊形 A.4.2.魏爾斯特拉斯多項式的牛頓多邊形 附錄五 奇點曲線的一個數值不變數 A.5.1.奇點的解析等價 A.5.2.奇點的次數 A.5.3.廣義類公式 A.5.4.廣義虧格公式 A.5.5.次和階 A.5.6.例子 附錄六 哈納克不等式 A.6.1.實代數曲線 A.6.2.連通分支和次數 A.6.3.係數在...
物理規律需要在一定的參考系表述出來。在狹義相對論提出以前,人們認為時間和空間是各自獨立的絕對的存在。自伽利略時代以來這種絕對時空的觀念就開始建立,牛頓創立的經典力學和運動定律就是在絕對時空觀的基礎上創立。在低速情況下這種觀點與實驗觀測符合的很好,但是在高速情況下絕對時空觀與客觀實際的矛盾就會顯現。十九...
q的非平凡加法特鱴和乘法特徵x_1,-,x_n相關聯的指數和,L(x_1,-,x_n,x,f;t)表示相應的L函式。本項目主要研究Adolphson和Sperber在1990年提出的關於L函式L(x_1,-,x_n,x,f;t)的牛頓多邊形的桓霾孿搿1狙芯肯釒坎喚鼉哂兄匾睦礪垡庖搴圖壑擔以諉藶胙е杏凶毆憷撓τ們熬啊 ...
起初牛頓和萊布尼茨以無窮小概念為基礎建立了微積分,後來因遇到邏輯困難,所以在他們的晚期都不同程度地接受了極限思想。牛頓用’路程的改變數ΔS‘與’時間的改變數Δt‘之比 “ ” 表示運動物體的平均速度,讓Δt無限趨近於零,得到物體的瞬時速度,並由此引出導數概念和微分學理論。他意識到極限概念的重要性,...
阿爾伯特·愛因斯坦在分析了以太假說的矛盾後,於1905年在《論動體的電動力學》中提出了兩條基本原理:狹義相對性原理和光速不變原理,並據此建立了狹義相對論(Special Theory of Relativity)。區別於牛頓的絕對時空觀,狹義相對論將時間和空間與觀測者視為一個不可分割的整體。相對桿和鐘分別靜止和勻速運動的觀測者...
