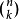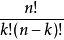二項式定理(英語:binomial theorem),又稱牛頓二項式定理,由艾薩克·牛頓於1664年、1665年間提出。該定理給出兩個數之和的整數次冪諸如展開為類似項之和的恆等式。二項式定理可以推廣到任意實數次冪,即廣義二項式定理。
基本介紹
- 中文名:二項式定理
- 外文名:binomial theorem
- 別稱:牛頓二項式定理
- 主要貢獻者:艾薩克·牛頓
- 最早研究時間:1664~1665年
- 適用領域範圍:初等代數學、組合數學
發展簡史,定理定義,二項式的矩陣形式,驗證推導,定理推廣,定理意義,與一元高次方程的關係,套用例子,
發展簡史
二項式定理最初用於開高次方。在中國,成書於1世紀的《九章算術》提出了世界上最早的多位正整數開平方、開立方的一般程式。11世紀中葉,賈憲在其《釋鎖算書》中給出了“開方作法本原圖”(如圖1),滿足了三次以上開方的需要。此圖即為直到六次冪的二項式係數表,但是,賈憲並未給出二項式係數的一般公式,因而未能建立一般正整數次冪的二項式定理。13世紀,楊輝在其《詳解九章算法》中引用了此圖,並註明了此圖出自賈憲的《釋鎖算書》。賈憲的著作已經失傳,而楊輝的著作流傳至今,所以今稱此圖為“賈憲三角”或“楊輝三角”。14世紀初,朱世傑在其《四元玉鑒》中復載此圖,並增加了兩層,添上了兩組平行的斜線(如圖2)。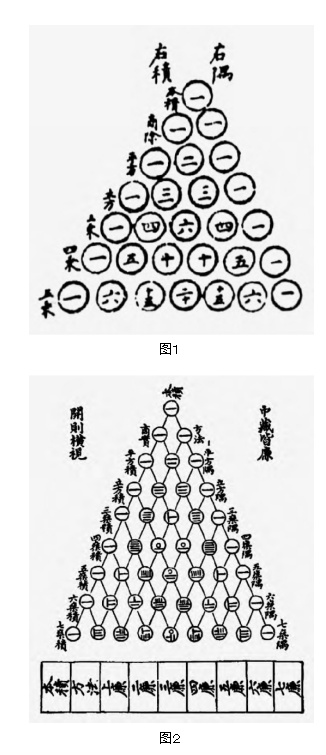

在阿拉伯,10世紀,阿爾 ·卡拉吉已經知道二項式係數表的構造方法:每一列中的任一數等於上一列中同一行的數加上該數上面一數。11~12世紀奧馬海牙姆將印度人的開平方、開立方運算推廣到任意高次,因而研究了高次二項展開式。13世紀納綏爾丁在其《算板與沙盤算法集成》中給出了高次開方的近似公式,並用到了二項式係數表。15世紀,阿爾 ·卡西在其《算術之鑰》中介紹了任意高次開方法,並給出了直到九次冪的二項式係數表,還給出了二項式係數表的兩術書中給出了一張二項式係數表,其形狀與賈憲三角一樣。16世紀,許多數學家的書中都載有二項式係數表。1654年,法國的帕斯卡最早建立了一般正整數次冪的二項式定理,因此算術三角形在西方至今仍以他的名字命名。1665年,英國的牛頓將二項式定理推廣到有理指數的情形。18世紀,瑞士的歐拉和義大利的卡斯蒂隆分別採用待定係數法和“先異後同”的方法證明了實指數情形的二項式定理。
定理定義
根據此定理,可以將x+y的任意次冪展開成和的形式
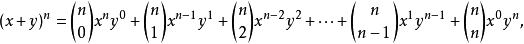
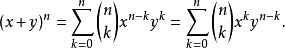
二項式的矩陣形式
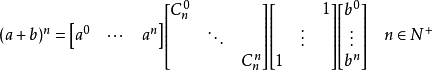
驗證推導
考慮用數學歸納法。
當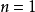 時,則
時,則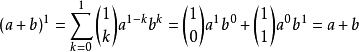
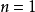
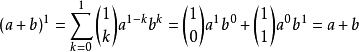
假設二項展開式在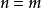 時成立。
時成立。
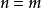
設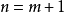 ,則有:
,則有:
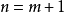

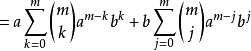
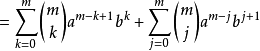
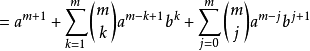
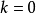
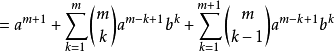
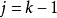
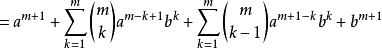
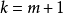
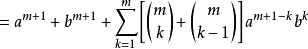
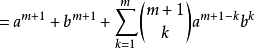
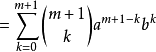
定理推廣
牛頓廣義二項式定理
二項式定理可以推廣到對任意實數次冪的展開。
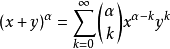
其中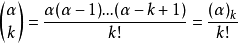 。
。
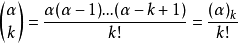
牛頓二項式擴充定理
設函式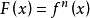
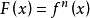
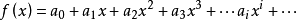
根據二項式定理,得F(x)的任意一項為:
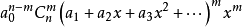
同理,上式中的任意一項為
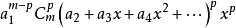
如此類推,我們預知最後一項存在;
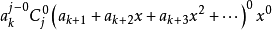
那么我們得到其中

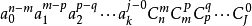
設M=0+j+....+q+p+m,而且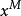 項的係數為AM
項的係數為AM
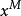
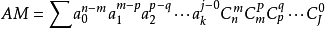
當x=1時,這就是多項式定理
二項式定理推廣至n為負數
二項式定理的一個常用形式為
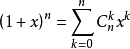
考慮到組合數的性質,上式可以改寫為
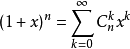
(n>0)
我們猜想當上式中左邊的指數為負整數時,公式
依然成立,即
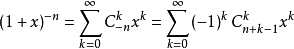
(n>0)
上式的正確性可以很容易地加以驗證。同理,二項式定理也可以推廣到非整數指數的情況。

上面的結果與牛頓二項式展開完全一致。
定理意義
這個定理在遺傳學中也有其用武之地,具體套用範圍為:推測自交後代群體的基因型和機率、推測自交後代群體的表現型和機率、推測雜交後代群體的表現型分布和機率、通過測交分析雜合體自交後代的性狀表現和機率、推測夫妻所生孩子的性別分布和機率、推測平衡狀態群體的基因或基因型頻率等。
與一元高次方程的關係
對於任意一個n次多項式,我們總可以只藉助最高次項和(n-1)次項,根據二項式定理,湊出完全n次方項,其結果除了完全n次方項,後面既可以有常數項,也可以有一次項、二次項、三次項等,直到(n-2)次項。特別地,對於三次多項式,配立方,其結果除了完全立方項,後面既可以有常數項,也可以有一次項。以最高次項係數為1的三次多項式為例,其配立方的過程如下:
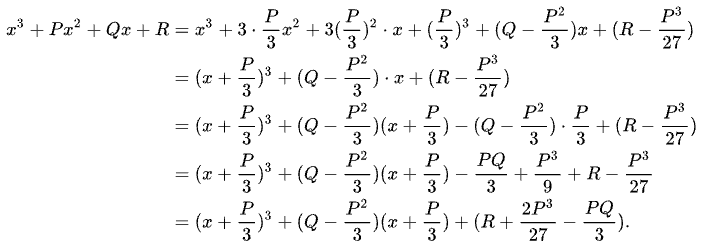
由於二次以上的多項式,在配n次方之後,並不能總保證在完全n次方項之後僅有常數項。於是,對於二次以上的一元整式方程,我們無法簡單地像一元二次方程那樣,只需配出關於x的完全平方式,然後將後面僅剩的常數項移到等號另一側,再開平方,就可以推出通用的求根公式。對於求解二次以上的一元整式方程,往往需要大量的巧妙的變換,無論是求解過程,還是求根公式,其複雜程度都要比一次、二次方程高出很多。
詳見:一元三次方程、一元四次方程。
套用例子
證明組合恆等式
二項式定理給出的係數可以視為組合數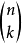 的另一種定義。 因此二項式展開與組合數的關係十分密切。 它常常用來證明一些組合恆等式。
的另一種定義。 因此二項式展開與組合數的關係十分密切。 它常常用來證明一些組合恆等式。
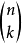
比如證明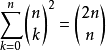 ,可以考慮恆等式
,可以考慮恆等式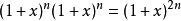 。
。
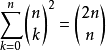
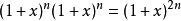
展開等式左邊得到: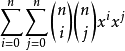 。 注意這一步使用了有限求和與乘積可以交換的性質。
。 注意這一步使用了有限求和與乘積可以交換的性質。
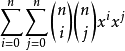
同時如果展開等式右邊可以得到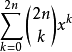 。
。
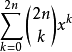
比較兩邊冪次位的項的係數可以得到: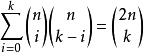 。
。
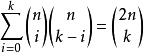
令 ,並注意到
,並注意到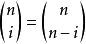 即可得到所要證明的結論。
即可得到所要證明的結論。

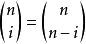
證明自然數冪求和公式
公式具體內容: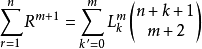
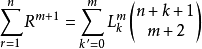
當n為奇數時,由1+2+3+4+...+N與s=N+(N-1)+(N-2)+...+1相加得:
2s=N+[1+(N-1)]+[2+(N-2)]+[3+(N-3)]+...+[(N-1)+(N-N-1)]+N
=N+N+N+...+N加或減去所有添加的二項式展開式數
=(1+N)N減去所有添加的二項式展開式數。
當n為偶數時,由1+2+3+4+5+...+N與s=N+(N-1)+(N-2)+...+1相加得:
2s=N+[1+(N-1)]+[2+(N-2)]+[3+(N-3)]+[4+(N-4)]...+[(N-1)+(N-N-1)]+N
=2N+2[(N-2)+(N-4)+(N-6)+...0或1]加或減去所有添加的二項式展開式數
又當n為偶數時,由1+2+3+4+5+6+...+N與s=N+(N-1)+(N-2)+...+1相加得:
2s=[N+1]+[(N-1)+2]+[(N-2)+3]+...+[(N-N-1)+(N-1)]
=2[(N-1)+(N-3)+(N-5)+...0或1]加或減去所有添加的二項式展開式數,合併n為偶數時2S的兩個計算結果,可以得到s=N+(N-1)+(N-2)+...+1的計算公式。