二項展開式

二項展開式是依據二項式定理對(a+b)ⁿ進行展開得到的式子，由艾薩克·牛頓於1664-1665年間提出。二項展開式是高考的一個重要考點。在二項式展開式中，二項式係數是一些特殊的組合數，與術語“係數”是有區別的。二項式係數最大的項是中間項，而係數最大的項卻不一定是中間項。

基本介紹

• 中文名：二項展開式
• 外文名：Binomial expansion
• 定理：二項式定理
• 提出者：艾薩克·牛頓
• 方法：特殊值法
• 套用：粗略的分析和估計以及證明恆等式

二項式定理

其中， ，又有 等記法，稱為二項式係數，此係數亦可表示為楊輝三角形。等式的右邊 即為 的展開式，稱為二項展開式。

理解

將 看成 個 相乘，從每個括弧中取一項 (非 即 ) 相乘的所有單項式合併同類項得到的，按取 的個數分為 類 ，不取 的是 ，取 1 個 的是 ，...， 取 個 的是 ，...，取 個 的是

注意：

（1）選取性，二項式的兩項怎樣選取 (各取幾個) 才能構成所求的項；

（2）有序性， 的展 開式第 項是取 個 (同時取 個 )， 這裡的 和 不能互換

（3）項 、項的係數與二項式係數的區別

某項要把這一項全部寫出來；某項的係數只寫這一項的係數，不帶字母 (即把每個字母當作數 1) ；某項的二項式係數就是相應的組合數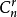

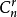
性質

（1）項數：n+1項

（2）第k+1項的二項式係數是

（3）在二項展開式中，與首末兩端等距離的兩項的二項式係數相等。

（4）如果二項式的冪指數是偶數，中間的一項的二項式係數最大。如果二項式的冪指數是奇數，中間兩項的的二項式係數最大，並且相等。

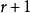（5）二項式通項：，是第項

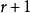
證明

這裡，採用數學歸納法對二項式定理進行證明

當 ，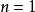

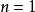
假設二項展開式在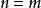 時成立，設 ，則：

（取出 的項）

（設 ）

（ 取出 項）

（兩者相加）

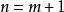（套用帕斯卡法則）

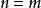
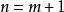
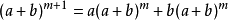
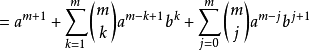
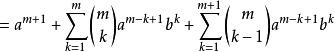
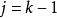
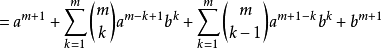
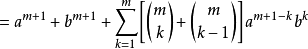
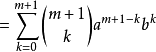
等式也成立

結論：對於任意自然數n，等式均成立。

例題

某項的係數

求二項展開式的某項或某項的係數是高考數學的一個基本知識點，每年的高考題都有一定的題出現。

例1. 求 的展開式中 的係數

解： 要取2個，故 的係數是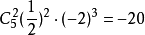

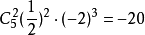
例2. 求 的展開式中 的係數

解： 要取4個，故的係數是

係數最值項

例. 求 展開式中係數最大項和最小項

解：

通項=

通項的係數=

設係數 最大，則

解得： ，因為，所以，故係數最大項為和

由於最大項在中間取得，所以最小項在兩端，計算得：，故係數最小項為

指定項

求二項展開式中的指定項，一般是利用通項公式進行。

例. 展開式中的常數項

解：展開式的通項=，令 ，解得

故常數項為：