二項式定理的展開式富有規律性、美觀性,體現了數學的美學文化,而多項式定理為二項式定理的推廣。用實際生活中的空盒放球來描述的話,則為:把 n 個有區別的小球放入到 k 個有區別的盒子中(盒內無序),使得第一個盒子裡邊裝有 n1 個小球,第二個盒子裡邊裝有 n2 個小球,…,第 t 個盒子裡邊裝有 nt個小球,並且滿足 n1+n2+...+nt=n,則可以很容易的利用多項式定理得到不同方法總的數目。
基本介紹
- 中文名:多項式定理
- 外文名:Multinomial theorem
- 提出者:德國數學家萊布尼茲
- 套用學科:代數,組合數學
- 本質:二項式定理的推廣
- 套用1:求解多項式展開式中某一項的係數
- 套用2:小球入盒問題
定義
預備知識




定理內容


定理證明


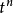




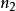


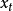


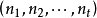
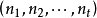


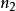


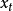




特殊情況



推論
推論1

推論2

推論3
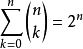
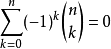
推論4