基本介紹
- 中文名:
- 外文名:
- 學科:
- 研究方向:
- 特徵:
- 學科性質:
原理結構


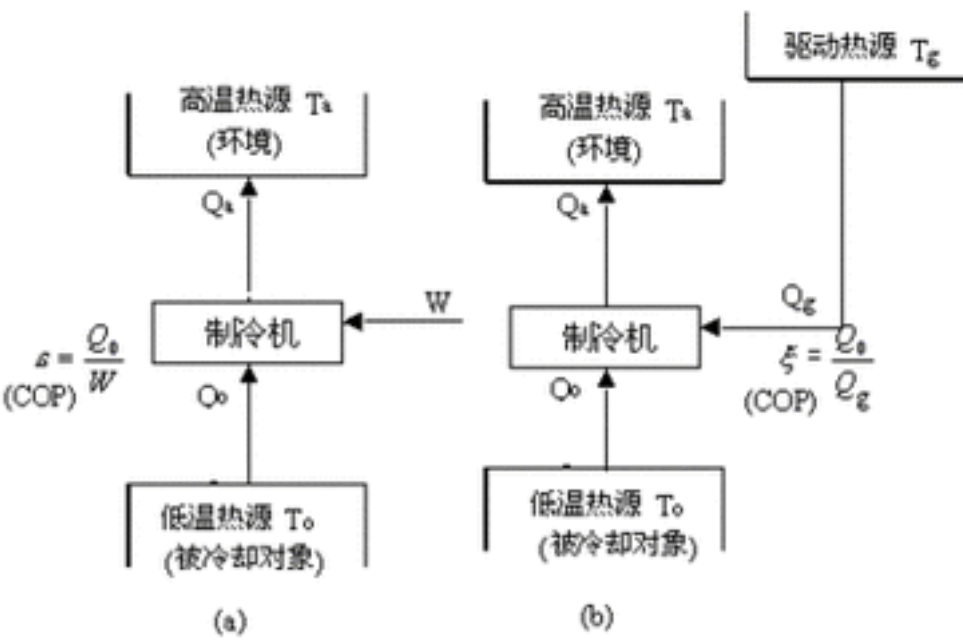



熱力學作為物理學的一個分支,是研究物質的熱運動、性質及其規律的學科。在我們的日常生活和工業生產實踐中到處充滿了熱力學定律套用的實例。熱力學是理工科,比如物理、化學、工程等學科的重要基礎課程之一,是機械、化工、航空、環境、...
它證實熵增加原理成立:達到平衡態的熱力學系統存在一個態函式熵,孤立系的熵不減少,達到平衡態時的熵最大。這就是說,熱力學第二定律要求:孤立系中發生的過程沿著熵增加的方向進行,稱為熵判據。它與熱力學第一定律和熱力學第三...
故稱為“第零定律”)熱力學基本方程 在熱力學定律中:第零定律給出了溫度T的定義;第一定律給出了能量守恆的關係;第二定律給出了熵增原理;第三定律告訴人們絕對零度無法達到。結合以上定律和公式,可以得出熱力學基本方程:
其中熱力學第零定律又稱為熱平衡定律,這是因為熱力學第一、第二定律發現後才認識到這一規律的重要性;熱力學第一定律是能量守恆與轉換定律在熱現象中的套用;熱力學第二定律有多種表述,也叫熵增加原理。發現理論 1901年,范霍夫因...
但是,若把系統內外一併考察仍然服從熵增原理。物體與熱力學定律 熱力學第零定律 A物體與B物體溫度相等,B物體與C物體溫度相等,則A物體與C物體溫度相等。熱力學第一定律 熱力學第一定律也叫能量守恆定律:自然界一切物質都具有能量,...
同時也形成了“工程熱力學”這門技術科學,它成為研究熱機工作原理的理論基礎,使內燃機、汽輪機、燃氣輪機和噴氣推進機等相繼取得迅速進展。與此同時,在套用熱力學理論研究物質性質的過程中,還發展了熱力學的數學理論,找到了反映物質...
以熵原理為核心的熱力學第二定律,歷史上曾被視為墮落的淵藪。美國歷史學家亞當斯H.Adams(1850-1901)說:“這條原理只意味著廢墟的體積不斷增大”。有人甚至認為這條定律表明人種將從壞變得更壞,最終都要滅絕。熱力學第二定律是當時...
這個定律非常重要,為化學平衡提供了根本性原理。吉布斯給出了熱力學原理的更為完美的表述形式,用幾個熱力學函式來描述系統的狀態,使化學變化和物理變化的描述更為方便和實用。他發表了著名的“相律”,對相平衡的研究起著重要的指導...
熵是熱力學中衡量系統狀態無規則性的一個狀態變數。對一個變化著的孤立系統而言,其熵總是增加的。熱力學第三定律是絕對零度不能達到原理。熱力學的三個定律是以直接觀測到的和由實驗得到的事實為基礎而總結出來的。因此熱力學理論及其...
熵(Entropy)起初是一個熱力學函式,後發展為系統混亂程度的度量,是一個描述系統熱力學狀態的函式。克勞修斯在《熱學之第二定律的修正形式》(Üeber eine veränderte Form des zweiten Hauptsatzes der mechanischen Wärmetheorie)...
這就是“熱力學法則”——熱量平衡原理。說到最後,減輕體重的唯一正道是從食物中攝入較少的能量,並且/或者消耗更多的能量。然而,僅有1/3減肥中的人在嘗試這一推薦減肥方法――少食多動,而它正是體重減輕的根本。
生活中無處不存在熱力學現象,熱力學現象的本質和原理亦來自生活。其實我們身邊經常可以看到很多和熱力學有關的現象,只是我們經常是不會去用學過的知識很好的聯繫和分析它。比如家裡用的空調,熱水器,抽水泵,高壓鍋等等,都是我們身邊...
熱力學第一定律在大氣科學中的數學表述。描述 大氣的動力學過程和熱力學過程是相互聯繫、相互制約的,熱力學第一定律也是套用於大氣運動的基本定律,它給出了系統狀態改變與熱量交換之間的關係。熱力學第一定律可表述為:物質體積元中內能...
熱力學能的絕對值難以確定,也無確定的必要,我們關心的是熱力學能的變化,只要終態始態一定,熱力學的變化量U是一定的。公式原理 構想向一個系統供熱,系統的溫度就要上升,這表明,系統的內能增加了, 其增加的量當然就等於系統吸收...
在物理學、化學系統中,熱傳導、擴散、電導、化學反應等是一些基本的非平衡現象,套用不可逆過程熱力學的原理討論這些現象,可以得到有意義的具體結果。在一些非平衡系統中,常常存在著多種不可逆過程的交叉現象。例如,在混合物體系中,...
套用熱力學原理選擇催化劑 根據物質和反應的熱力學特徵選擇催化劑 鑒於多相催化理論的現狀,尚不能完全根據理論來選擇催化劑。要找到一種能在工業上套用的新催化劑,主要靠實踐經驗和大量的篩選工作。許多催化工作者注意到用熱力學原理選擇...
過程熱力學分析內容 化工生產中,人們總是希望能夠合理、充分的利用能源,提高能源的利用率,以獲得更多的功。根據熱力學的基本原理,闡述了理想功、損失功、有效能等一些基本概念和計算,以便評定實際生產過程的能量利用情況,我提高能量...
以熵原理為核心的熱力學第二定律,歷史上曾被視為墮落的淵藪。美國歷史學家亞當斯H.Adams(1850-1901)說:“這條原理只意味著廢墟的體積不斷增大”。有人甚至認為這條定律表明人種將從壞變得更壞,最終都要滅絕。熱力學第二定律是當時...
值得重視的是,1931年,在微觀可逆性原理的基礎上,昂塞格把巨觀與微觀的物理概念結合起來,推導出“昂塞格倒易關係”。1947年普利高津提出了最小熵生產原理。這二者是不可逆過程熱力學的理論基礎。不可逆熱力學主要是研究近平衡態的線性...
這個規律叫做熵增加原理。熵的增加表示系統從幾率小的狀態向幾率大的狀態演變,也就是從比較有規則、有秩序的狀態向更無規則、更無秩序的狀態演變。熱力學第三定律 此定律指出,構想通過幾個有限的步驟使物體冷卻到絕對零度,是不可能的...
熱功相當原理跟微粒說(唯動說)結合則導致了分子運動論的建立。而在這段時期內唯象熱力學和分子運動論的發展還是彼此隔絕的。第三時期內唯象熱力學的概念和分子運動論的概念結合的結果,最終導致了統計熱力學的產生。它開始於19世紀70...
化學熱力學是物理化學中最早發展起來的一個分支學科,主要套用熱力學原理研究物質系統在各種物理和化學變化中所伴隨的能量變化、化學現象和規律,依據系統的巨觀可測性質和熱力學函式關係判斷系統的穩定性、變化的方向和限度。熱力學的歷史...
它用於描述物體的發射率與吸收比之間的關係。在熱力學平衡的條件下,各種不同物體對相同波長的單色輻射出射度與單色吸收比之比值都相等,並等於該溫度下黑體對同一波長的單色輻射出射度。詳細內容 熱輻射的基本概念 任何物體在發出輻射能的...
熵的絕對值不能由熱力學第二定律確定。可根據量熱數據由第三定律確定熵的絕對值,叫規定熵或量熱法。還可由分子的微觀結構數據用統計熱力學的方法計算出熵的絕對值,叫統計熵或光譜熵。熵增原理 熵增原理就是孤立熱力學系統的熵不...
我國學者首次提出了能源轉換利用與CO2分離一體化原理,實現低能耗甚至無能耗分離CO2,研究制定了適合我國國情的溫室氣體控制技術路線。熱機氣動熱力學與流體機械分學科 國際上現已採用三維粘性計算流體動力學設計航空發動機諸部件,尤其是葉輪...
傳熱是指由於溫度差引起的能量轉移,又稱熱傳遞。由熱力學第二定律可知,凡是有溫度差存在時,熱就必然從高溫處傳遞到低溫處,因此傳熱是自然界和工程技術領域中極普遍的一種傳遞現象。無論在能源、宇航、化工、動力、冶金、機械、建築等...
