基本介紹
- 中文名：無模型自適應控制
- 外文名：Model-free adaptive control, MFAC
- 方法：自適應控制方法
- 特點：僅利用受控系統的輸入輸出數據進行控制器的設計和分析
簡介,過程辨識,控制器設計,系統穩定性,功能配置,算法特點,
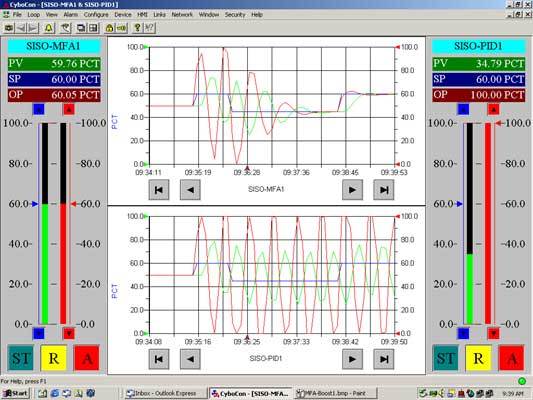
簡介
針對一類離散時間非線性系統的無模型自適應控制方法是於1994年提出來的。該方法使用了一種新的動態線性化方法及一個稱為偽偏導數（pseudo-partial derivative，PPD）的新概念，在閉環系統的每個動態工作點處建立一個等價的動態線性化數據模型，然後基於此等價的虛擬數據模型設計控制器並進行控制系統的理論分析，進而實現非線性系統的自適應控制。PPD參數可僅使用被控對象的I/O量測數據進行估計。動態線性化方法有三種具體形式，分別為緊格式動態線性化、偏格式動態線性化和全格式動態線性化。
過程辨識
對於傳統的自適應控制方法，如果不能獲得過程的定量信息，一般需要採用某種辨識機制，以線上或離線的方式獲得系統的動態特性。由此產成了以下一些難以解決的問題：
· 需要離線學習；
· 辨識所需的不斷的激勵信號與系統平穩運行的矛盾；
· 模型收斂和局部最小值問題；
· 系統穩定性問題。
基於辨識的控制方法不適用於過程控制的主要原因是控制和辨識是一對矛盾體。好的控制使系統處於一個穩定狀態，這種情況下設定值（SP）、控制器輸出（OP）和過程變數（PV）在趨勢圖中顯示出來的都是直線。任何穩定系統都會達到另一個穩定狀態，而其中的過程動態特性的變化卻不能被察覺，因此通常需要施加激勵信號來進行有效的過程辨識。然而，實際生產過程很難容許這樣做。
MFAC控制系統中沒有辨識環節因此可以避免上述問題。一旦運行，MFAC控制器就可立刻接管控制。MFAC控制器中刷新權值的算法是基於一個單一的目標，即縮小設定值和過程變數之間的偏差。這意味著當過程處於穩定狀態，偏差接近零時，不需要對MFAC控制器的權值進行修改。
控制器設計
PID控制器仍然被廣泛使用的主要原因就在於它是一種通用型控制器，無需進行專門的控制器設計。為特殊的套用設計控制器需要有豐富的經驗。由於大多數先進控制器是基於模型的，其通用型性不夠，所以儘管這些方法已經有三四十年的歷史了，至今還不能在過程控制領域得到廣泛的套用。
MFAC控制器是通用型控制器，並已經開發出一系列MFAC控制器用於控制各種問題迴路。如SISO MFAC控制器可直接取代PID，免去了複雜的控制器參數整定；非線性MFAC控制器能控制極端非線性過程；抗滯後MFAC控制器能控制大滯後過程；MIMO MFAC控制器能控制多變數過程；前饋MFAC控制器能抑制可測的擾動；以及魯棒MFAC控制器能迫使過程變數維持在預定的範圍。
MFAC控制器的用戶，無需對控制器進行設計，只要選擇相應的控制器並簡單地設定控制器參數就可以將MFAC控制器投入使用。這是無模型自適應控制器與其它基於模型的先進控制器的一個主要區別。
控制器參數整定
自適應控制器不需要人工整定參數，無模型自適應控制器真正實現了這一點。無需參數整定，MFA就能自適應過程動態特性的變化並克服潛在的擾動以滿足新的操作條件。用戶友好的MFA控制器保留了一些參數允許用戶及時地調整控制效果。
系統穩定性
控制系統的閉環穩定性對於控制器是否實用是非常重要的。如果掌握了閉環控制系統的穩定性判據，就可以利用它來判斷控制系統能否安全地投入使用。如圖1所示，傳統的基於模型的自校正控制系統主要由三個部分組成：控制器、過程和模型。這裡模型是指可以描述過程輸出和輸入關係的數學表達式，通常是通過辨識器來建立的。辨識器利用過程輸入輸出的數據通過一定的學習算法減小模型的偏差em(t)（PV與模型輸出y2(t)之間的偏差）。
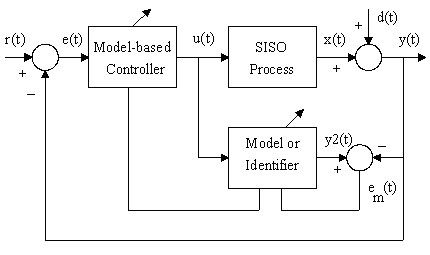 基於模型的自適應控制系統 | 符號： r(t) – 設定值 u(t) – 控制器輸出 y(t) – 過程變數 x(t) – 過程輸出 d(t) – 干擾 e(t) – 偏差 e(t) = r(t) - y(t) y2(t) – 模型輸出 em(t) – 模型偏差 em(t) = y2(t) - y(t) |
圖1. 基於模型的自適應控制系統
在這個系統中，整個閉環系統的穩定性與過程、控制器和模型有著以下幾個方面的聯繫：
· 假設過程是穩定的（即過程開環穩定）；
· 控制迴路的穩定性是由模型的收斂性來保證的；
· 模型的收斂性需要控制迴路穩定並持續地發出激勵信號。
這幾個條件形成了一個難以解決的死圈。因此，基於模型的自適應控制系統沒有通用的穩定性判據。也就是說，每次使用基於模型的自適應控制器前，不得不分析它的穩定性。顯然，這也是使用基於模型的自適應控制方法的一個主要技術壁壘。
相比之下，由於MFA不存在辨識環節，因此論證出了一個通用的系統穩定性判據。即，只要是一個無源過程（本身不產生能量或熱量的過程），閉環MFA控制系統的穩定性就可以得到保證，過程可以是線性/非線性，定常/時變等等。燃燒過程時一個無源的過程，其熱量的產生是由燃料燃燒帶來的。
單迴路MFAC控制系統結構
單輸入單輸出（SISO）MFAC控制系統的結構如圖2所示。其結構同傳統的單迴路控制系統一樣簡單，包括一個單輸入單輸出過程，一個MFAC控制器和一個反饋迴路。
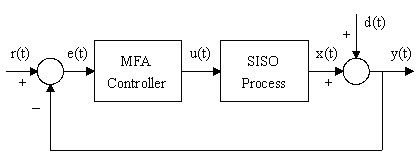 單迴路MFA控制系統 | 符號： r(t) – 設定值，SP u(t) – 控制器輸出，OP y(t) – 過程變數，PV x(t) – 過程輸出 d(t) – 干擾 e(t) – 偏差 e(t)=r(t)-y(t) |
圖2. 單迴路MFA控制系統
控制目標
這種控制器的控制目標是產生一個輸出u(t)，迫使過程變數y(t)在設定值變化，存在擾動和過程動態特性改變的情況下仍然能跟蹤設定值r(t)。也就是，MFAC控制器以線上的方式不斷減小設定值r（t）和過程變數y(t)之間的偏差e(t)。根據以下兩點使偏差e(t)最小：（i）MFAC控制器的調節控制能力；（ii）不斷調整MFAC控制器的權重因子，使得控制器有能力處理過程動態特性的改變，擾動和其它不確定因數。
與圖1相比，MFAC控制系統沒有過程模型和辨識器。因此也沒有模型偏差em(t)，只有設定值（r(t)或SP）和過程變數（y(t)或PV）之間的偏差e(t)是控制目標。
MFAC控制器結構
在這個神經網路中有一組可以根據需要而改變的權重因子（Wij和hi），從而對控制器的行為進行調整。更新權重因子的算法是以縮小設定值與過程變數之間的偏差為目標。由於其效果與控制目標是一致的，因此，採用權重因子能幫助控制器在過程動態特性發生變化的時候減小偏差。
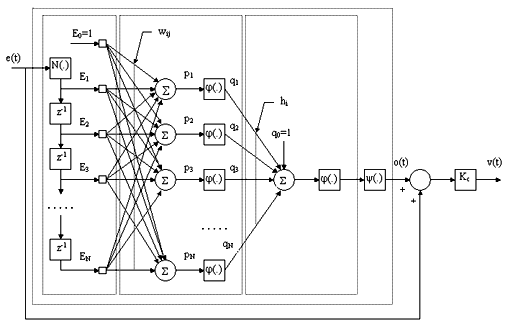
SISO MFAC控制器結構
圖3. SISO MFAC控制器結構
此外，基於人工神經網路的MFAC控制器保存了一部分歷史數據，為了解過程動態特性提供有價值的信息。相比之下，數字式PID控制器只保留當前的和之前的2個採樣數據。在這一點上，PID控制器幾乎沒有任何記憶能力，而MFA擁有一個“聰明”的控制器所必需的記憶能力。
MFA控制系統的要求
作為一個反饋控制系統，MFAC對被控對象有以下幾點要求：
· 過程對象可控；
· 開環穩定；
· 正作用或反作用（過程不變方向）。
對於不可控的過程對象，則需要改進過程的結構或匹配系統變數。
對於開環不穩定的過程對象，則需使它先穩定下來。不過，對於某些開環不穩定的過程，如無自衡的液位迴路，使用MFA時就不需要進行特殊的處理。
對於在操作範圍內變方向的過程，則需要特殊的MFA控制器。僅需簡單地配置少量的MFA控制器的參數。
基於MFAC核心控制技術，針對特殊的控制問題，設計了多種MFAC控制器：
· SISO MFA控制器（標準MFAC） － 取代PID，免去了複雜的控制器參數整定；
· 非線性MFAC控制器（Nonlinear MFAC） － 控制極端非線性過程；
· MFAC pH控制器 － 控制pH過程；
· 前饋MFAC控制器（Feedforward MFAC） － 抑制可測的擾動；
· 抗滯後MFAC控制器（Anti-delay MFAC） － 控制大滯後過程；
· 魯棒MFAC控制器（Robust MFAC） － 迫使過程變數維持在預定的範圍；
· 時變MFAC控制器（Time-varying MFAC） － 控制大慣性、滯後時間不確定的過程；
· 抗滯後MFAC pH控制器（Anti-delay MFAC pH） － 控制大致滯後的pH過程；
