常微分方程穩定性理論的重要概念之一,其兩種定義方式詳見正文。
模組化多電平變流器相間環流的存在使得橋臂電流產生畸變,一方面增加了變流器的損耗,另一方面對功率器件的安全工作範圍也提出了更高的要求。
基本介紹
- 中文名:漸進穩定性
- 外文名:asymptotic stability
- 相關概念:李雅普洛夫穩定性
- 領域:常微分方程
定義
定義一
定義二
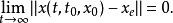
李雅普洛夫穩定性
定義1
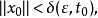
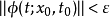
定義2
定義3
平衡狀態
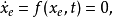
常微分方程穩定性理論的重要概念之一,其兩種定義方式詳見正文。
模組化多電平變流器相間環流的存在使得橋臂電流產生畸變,一方面增加了變流器的損耗,另一方面對功率器件的安全工作範圍也提出了更高的要求。
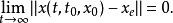
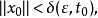
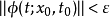
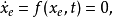
常微分方程穩定性理論的重要概念之一,其兩種定義方式詳見正文。模組化多電平變流器相間環流的存在使得橋臂電流產生畸變,一方面增加了變流器的損耗,另一方面對功率器件...
全局漸近穩定性(global asymptotic stability)是指一類全相空間均為吸引區域的漸近穩定性。對於線性系統而言,一個線性系統如果是漸近穩定的,則必然是全局漸近穩定的。...
漸進穩定狀態,是指人或事物表現出來的形態逐步前進、發展沒有變動。... 漸進穩定狀態判據的懸浮控制系統穩定性分析 編輯 在分析懸浮控制系統工作原理的基礎上,建立...
在自動控制領域中,李雅普諾夫穩定性(英語:Lyapunov stability,或李亞普諾夫穩定性)可用來描述一個動力系統的穩定性。如果此動力系統任何初始條件在平衡態附近的軌跡均...
絕對穩定性研究在某種限制下的一類非線性系統為全局漸近穩定的條件,而通常意義下的穩定性則只局限於對具體的非線性系統個別進行分析。非線性特性可在一個限制類中...
李雅普諾夫穩定性理論是俄國數學家和力學家A.M.李雅普諾夫在1892年所創立的用於分析系統穩定性的理論。...
《穩定性與魯棒性的理論基礎》是一本正文語種為簡體中文的書籍。... 1.8 時變系統的一致漸近穩定(Matrasov定理)1.9 一致漸近穩定的反問題1.10 力學系統穩定性...
穩定魯棒控制(Stable robust control)方面的研究始於20世紀50年代。在過去的20年中,穩定魯棒控制一直是國際自控界的研究熱點。所謂“魯棒性”,是指控制系統在一定(...
漸進式訓練系統由四大系列產品組成。分別是彈性阻力訓練系列、平衡與穩定性訓練系列、手部功能訓練系列、水中力量訓練系列。...
李亞普諾夫方程,或稱李亞普諾夫矩陣方程,是指對於沒有外部輸入的線性定常連續系統,用以構造李亞普諾夫函式的方程,或使系統原點平衡狀態漸進穩定的充分必要條件。其...
6.1.2 基本再生數和可行平衡點的局部漸近穩定性 1886.1.3 全局漸近穩定性 1926.1.4 結論 1956.2 具有胞內時滯和飽和發生率的HIV-1感染動力學模型 196...
