漸近無偏估計量(asymptotic unbiased estimator)是指當樣本容量n 無限增大時,近似無偏的估計量。
基本介紹
- 中文名:漸近無偏估計量
- 外文名:asymptotic unbiased estimator
- 所屬學科:數學
- 所屬領域:統計學
- 相關概念:估計量、方差、數學期望等
定義
無偏性與漸近無偏估計量










例題分析















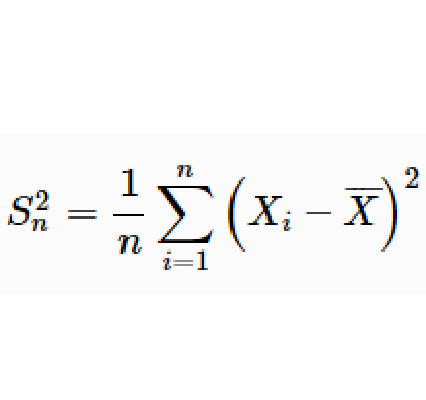
漸近無偏估計量(asymptotic unbiased estimator)是指當樣本容量n 無限增大時,近似無偏的估計量。

























漸近無偏估計量(asymptotic unbiased estimator)是指當樣本容量n 無限增大時,近似無偏的估計量。...
亦稱近似無偏估計。 ... 漸近無偏估計編輯 鎖定 討論 本詞條缺少信息欄、概述圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!亦稱近似無偏估計。 [1...
無偏估計是用樣本統計量來估計總體參數時的一種無偏推斷。估計量的數學期望等於被估計參數的真實值,則稱此估計量為被估計參數的無偏估計,即具有無偏性,是一種...
漸近有效無偏估計是一種參數估計方法.它是對隨機向量的聯合機率密度函式中未知參數的一種估計...
無偏估計值,樣本估計量的期望值等於真實值 。... 但最大似然估計值σ′2不是σ2的無偏估計值,而只是其漸近無偏估計值。用無偏估計值來估計參數時沒有系統...
若 ,則稱 為一致性估計值。在一定條件下,最小二乘估計是最優線性無偏估計,它的估計值是有效估計,而且是一致性估計。極大似然估計在一定條件下漸近有效,而且是...
顯然,設m為有限值,當N→∞,則從式(2)可以得到漸近無偏估計。計算m個滯後數時的自相關估計約需Nm次實數乘加運算。 間接算法 間接方法是利用快速傅立葉變換的...
估計量的無縮性和最小方差性,是優良估計量的兩個可要標誌。因此,稱最小方差無偏估計為最優估計。然而,由於樣本的隨機性,任何估計量的方差也不能任意地小。...
其特點是測向解析度高;對信號個數、DOA、極化、噪聲干擾強度、來波的強度和相干關係可以進行漸近無偏估計;可以解決多徑信號的DOA估計問題;可以用於高密度信號環境下...
1.6最小二乘估計量的統計性質 1.6.1線性特性 1.6.2無偏性 1.6.3最小方差性 1.6.4漸近無偏性 1.6.5一致性 1.7最小二乘回歸函式的性質 1.8擬合優度的測量...
技術性注釋第2章 估計量標準2.1 引言2.2 計算成本2.3 最小二乘2.4 R2最大2.5 無偏性2.6 有效性2.7 均方誤差(MSE)2.8 漸近性2.9 最大似然...
還有漸近無偏性、漸近有效性(見點估計)、和漸近正態性,或更一般地,漸近於某種特殊的極限分布的性質,也都是重要的大樣本性質。大樣本統計的發展,依賴於機率論的...
當平穩序列的譜分布函式F(λ)具有譜密度ƒ(λ)(即功率譜)時,可用(2π)-1I(λ)去估計ƒ(λ),它是ƒ(λ)的漸近無偏估計。如欲求ƒ(λ)的相合...
《數理統計:基本思想和選題(第1卷)(第2版·影印版)》內容豐富,視野開闊,知識面寬,涵蓋了統計量——樣本空間的函式;多參數指數族的極大似然估計;無偏估計與...
1.4 高階累積量的性質 第2章 非參數化高階譜分析 2.1 BR高階譜估計子 2.1.1 定義與假設 2.1.2 BR估計子 2.1.3 BR估計子的漸近無偏性 2.2 Zurb...
§3.1 點估計的漸近性質 §3.2 充分完全統計量 A充分統計量 B.完全統計量 C.指數族分布 D.指數族分布的自然形式 §3.3 最小方差無偏估計 A.估計量的評價...
1.4 統計量與抽樣分布1.5 充分統計量1.6 習題第二章 參數點估計2.1 估計量求法2.2 一致最小方差無偏估計2.3 同變估計2.4 估計量的漸近性質2.5 習題...
第2章 參數估計理論372.1 估計子的性能372.1.1無偏估計與漸近無偏估計382.1.2 估計子的有效性402.2 Fisher信息與Cramer-Rao不等式 42...
