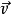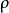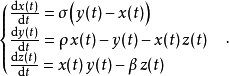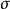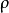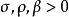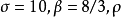洛倫茨吸引子

洛倫茨吸引子是洛倫茨振子（Lorenz oscillator）的長期行為對應的分形結構，以愛德華·諾頓·洛倫茨的姓氏命名。

基本介紹

簡述,洛倫茨方程,瑞利數,原始碼,GNU Octave,Borland C,參見,

簡述

洛倫茨吸引子及其導出的方程組是由愛德華·諾頓·洛倫茨於1963年發表，最初是發表在《大氣科學雜誌》（Journal of the Atmospheric Sciences）雜誌的論文《Deterministic Nonperiodic Flow》中提出的，是由大氣方程中出現的對流卷方程簡化得到的。
這一洛倫茨模型不只對非線性數學有重要性，對於氣候和天氣預報來說也有著重要的含義。行星和恆星大氣可能會表現出多種不同的準周期狀態，這些準周期狀態雖然是完全確定的，但卻容易發生突變，看起來似乎是隨機變化的，而模型對此現象有明確的表述。
從技術角度看來，洛倫茨振子具有非線性、三維性和確定性。2001年，沃里克·塔克爾（Warwick Tucker）證明出在一組確定的參數下，系統會表現出混沌行為，顯示出人們今天所知的奇異吸引子。這樣的奇異吸引子是豪斯多夫維數在2與3之間的分形。彼得·格拉斯伯格（Peter Grassberger）已於1983年估算出豪斯多夫維數為2.06 ± 0.01，而關聯維數為2.05 ± 0.01。
此系統也會出現在單模雷射和發電機的簡化模型中。除此之外，閉環對流、水輪轉動等物理模型也有此系統的套用。
洛倫茨吸引子是洛倫茨振子（Lorenz oscillator）的長期行為對應的分形結構，以愛德華·諾頓·洛倫茨的姓氏命名。洛倫茨振子是能產生混沌流的三維動力系統，是一種吸引子，以其雙紐線形狀而著稱。映射展示出動力系統（三維系統的三個變數）的狀態是如何以一種複雜且不重複的模式，隨時間的推移而演變的。

洛倫茨方程

洛倫茨方程是基於納維－斯托克斯方程、熱傳導方程和連續性方程簡化得出，最初的形式為：
——流速，T——流體溫度，T0——上限溫度，
——密度，p——壓強，
——重力，
——依次為熱膨脹係數、熱擴散率和動黏滯係數。
簡化後的形式稱為洛倫茨方程，是決定洛倫茨振子狀態的方程為一組常微分方程：
含時間參數的形式：
稱為普蘭特爾數，
稱為瑞利數。所有的
，但通常
不定。

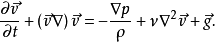
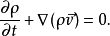
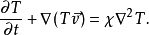
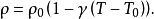
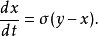
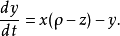
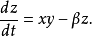
瑞利數

不同ρ值時的洛倫茨吸引子
ρ=14, σ=10, β=8/3（放大）
ρ=13, σ=10, β=8/3（放大）
ρ=15, σ=10, β=8/3（放大）
ρ=28, σ=10, β=8/3（放大）
ρ值較小時，系統是穩定的，並能演變為兩個定點吸引子中的一個；當ρ大於24.74時，定點變成了排斥子，會以非常複雜的方式排斥軌跡，演變時自身從不交叉。

原始碼

GNU Octave

下面是GNU Octave模擬洛倫茨吸引子的原始碼：
## Lorenz Attractor equations solved by ODE Solve## x' = sigma*(y-x)## y' = x*(rho - z) - y## z' = x*y - beta*zfunction dx = lorenzatt(X)    rho = 28; sigma = 10; beta = 8/3;    dx = zeros(3,1);    dx(1) = sigma*(X(2) - X(1));    dx(2) = X(1)*(rho - X(3)) - X(2);    dx(3) = X(1)*X(2) - beta*X(3);    returnend## Using LSODE to solve the ODE system.clear allclose alllsode_options("absolute tolerance",1e-3)lsode_options("relative tolerance",1e-4)t = linspace(0,25,1e3); X0 = [0,1,1.05];[X,T,MSG]=lsode(@lorenzatt,X0,t);TMSGplot3(X(:,1),X(:,2),X(:,3))view(45,45)

Borland C

#include <graphics.h>#include <conio.h>void main(){    double x = 3.051522, y = 1.582542, z = 15.62388, x1, y1, z1;    double dt = 0.0001;    int a = 5, b = 15, c = 1;    int gd=DETECT, gm;    initgraph(&gd, &gm, "C:\\BORLANDC\\BGI");    do {    x1 = x + a*(-x+y)*dt;    y1 = y + (b*x-y-z*x)*dt;    z1 = z + (-c*z+x*y)*dt;    x = x1;    y = y1;    z = z1;    putpixel((int)(19.3*(y - x*0.292893) + 320),    (int)(-11*(z + x*0.292893) + 392), 9);    } while (!kbhit());    closegraph();}

參見

  • 混沌映射列表
  • Takens定理
  • 曼德布洛特集合

相關詞條

熱門詞條

聯絡我們