基本介紹
- 中文名:波群
- 外文名:wave group
- 領域:力學
- 產生原因:波的調製或包絡
- 地點:經常出現在海洋
- 相關名詞:波阻
簡介
定義和解釋
定義

推導




分散中的高階項

其他表達形式
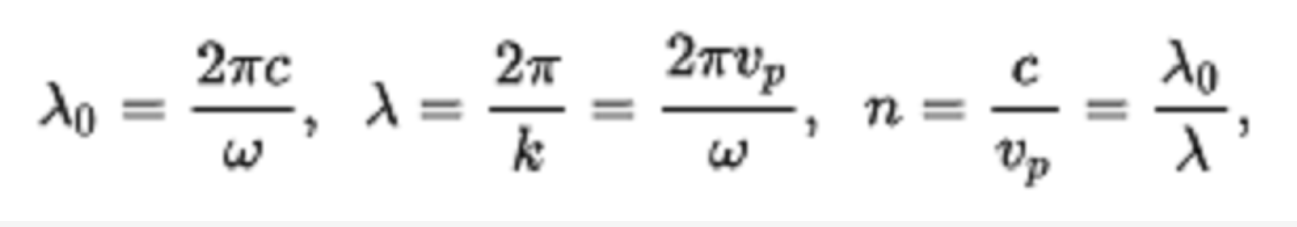

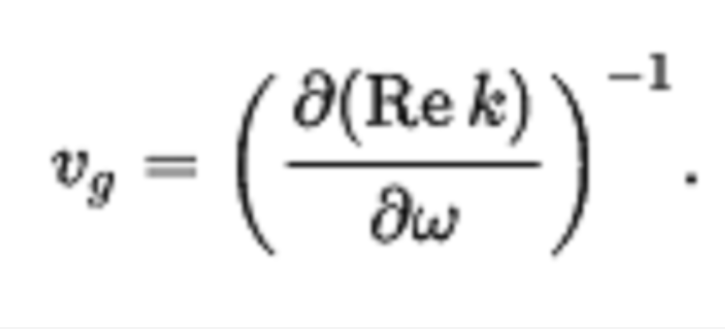






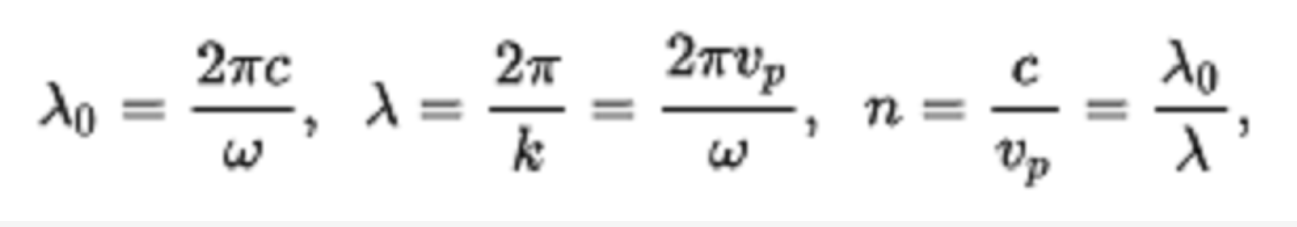

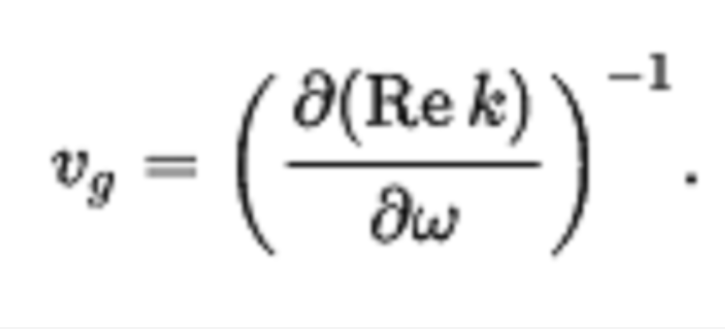
波群是波的幅度的整體形狀(稱為波的調製或包絡)通過空間傳播的現象。在實際的海洋中,經常可以觀察到這樣一種現象,其主要特徵是在固定地點,有時出現振幅大的波動,...
QRS波群反映左、右心室除極電位和時間的變化,第一個向下的波為Q波,向上的波為R波,接著向下的波是S波。自QRS波群起點至QRS波群終點的時間為QRS時限。QRS波群...
當心房到心室的傳導出現阻滯,則表現為PR間期的延長或P波之後心室波消失。 3.QRS波群 激動向下經希氏束、左右束枝同步激動左右心室形成QRS波群。QRS波群代表了...
相速是波包中某個單頻的相位移動速度=ω/k (k為波數,電磁學中,波數等於2π除以波長)。波的相速度或相位速度,或簡稱相速,是指波的相位在空間中傳遞的速度...
是指來自同一起搏點的心搏的心電圖形態和/或電壓甚至極性呈交替性變化。心房、心室除極和復極的各波段如P波、QRS波群、ST段、T波、U波等均可能發生電交替,...
房室交界性逸搏之心電圖表現為在長於正常PP間期的間歇後出現一個正常的QRS波群,此時因潛在起搏點發放的衝動誘發的逆行P波可以缺失或位於QRS波群之前或之後。...
2.QRS波群寬大畸形,時限>0.12秒,T波與QRS波群主波方向相反。 3.如能發現P波,則P波頻率比QRS波群慢,且P波與QRS波群之間無固定關係。 4.有時室上性激動...
心電圖表現為在較正常PP間期長的間歇後出現一個正常的QRS波群,P波缺失,或逆行P波位於QRS波之前或之後,此外亦可見到未下傳至心室的竇性P波。...
率依賴性心室內傳導改變時,QRS波群畸形。房顫波可粗可細,有時在V1導聯上可見到粗而較規則的顫動波,又稱為心房撲動顫動或不純撲動。顫動波也可細到在大多數...
1、QRS波群正常,心律規整,P'波形態異常,P'-R>0.12秒者為房性 室上性心動過速心電圖 ;有逆行的P'波或P'-R<0.12秒者為房室交接處性。多數情況下因...
QRS波群:典型的QRS波群包括三個緊密相連的波,第一個向下的波稱為Q波,繼Q波後的一個高尖的直立波稱為R波,R波後向下的波稱為S波。因其緊密相連,且反映了...
PR間期正常,QRS波群增寬,有預激波。預激綜合徵室上性心動過速發作時,預激表現大多消失,心電圖表現為QRS波群形態正常的室上性心動過速。並發房撲或房顫時,QR...
1.典型預激綜合徵:(1)P-R間期0.11秒;(3)QRS波群起始部分變粗鈍,稱為預激波或δ波;(4)繼發性ST-T改變。臨床上又分為三型: A型預激:預激波和QRS波...
衝動部分經旁路快速下傳,提前到達旁路的心室端,激動鄰近心肌,從而造成心室提前激動和改變心室肌正常興奮順序,其結果是心電圖上QRS波群畸形,起始部分有預激波(δ波...
心室奪獲和室性融合波的出現是診斷室速的有力證據。 5.QRS波形態與不發作時室早的形態一致。 6.雙向性室性心動過速表現為寬大畸形的QRS波群主波方向一上一...
1、心電向量:心電活動不論是右、左心房(P波),或是代表啟動心室搏動的心電活動(QRS波群),都是既有方向,又有大小(量)的心電活動,就稱為心電向量。它反映...
房室旁道順行傳導引起:①PR間期縮短(<0.12秒);②QRS波群升支起始部粗純(delta波)和③QRS波群增寬的典型心電圖改變。這種圖形代表通過旁道的和通過希斯-浦...
完全左束支傳導阻滯的心電圖特點有以下幾點: ①QRS波群的時限≧0.12秒;②QRS波群的形態的改變:V5導聯呈寬大、平頂或有切跡的R波。凡是在v5或v6導聯R波之...
5)心室奪獲與室性融合波室性融合波、心室奪獲、全部心前區導聯QRS波群主波方向呈同向性等心電圖表現提示室性心動過速三、室顫...
二度房室傳導阻滯可分兩型:①二度Ⅰ型(文氏型) 心電圖表現為PR間期逐漸延長直至QRS波群脫落(P波不能下傳),RR間期逐漸縮短直至一個P波不能下傳,包含受阻P...
室內差異傳導是一個在心臟專業醫學角度,當心電圖上出現寬大畸形的QRS波群的專業學術用語。指當竇性或室上性激動通過抵達心室,此時心室內傳導組織尚未完全恢復應激與...
