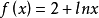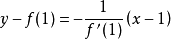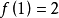相關詞條
- 法線方程
對於直線,法線是它的垂線;對於一般的平面曲線,法線就是切線的垂線;對於空間圖形,是垂直平面。...
- 數學要項定理公式證明辭典
3·2 法線方程 3·3 速度與加速度·平面上點的運動 3·4 其他套用 4.關於導函式的定理 4·1 羅爾定理 4·2 微分學中值定理 4·3 柯西中值定理 5.函式...
- 光學原理教程
主要內容包括:光的波動性及傳播規律,光的電磁理論基礎,平面波、球面波以及光在介質分界面上的傳播特性;光波在晶體中的傳播規律,晶體波面法線方程和折射率橢球方程,...
- 高等數學進階
題型12求空間曲線的切線方程和法平面方程(311);題型13求曲面的切平面方程和法線方程(313)8.4多元函式連續、偏導數與全微分及其套用考研真題3138.5本章練習題答案與...
- 2013考研數學大綱配套1000題
8.求空間曲面的切平面與法線方程、空間曲線的切線與法平面方程 二、單元檢測 第六章多元函式積分學 一、常考問題與方法技巧 1.考查二重積分的性質問題 2.交換積...
- 多元微積分學
第二節 空間曲線的切線與法平面方程第三節 曲線的弧長與平面曲線族的包絡一、曲線的弧長二、平面曲線族的包絡第四節 曲面的切平面與法線方程...
- 考研數學一大綱
1.理解導數和微分的概念,理解導數與微分的關係,理解導數的幾何意義,會求平面曲線的切線方程和法線方程,了解導數的物理意義,會用導數描述一些物理量,理解函式的可導...
- 大學生數學手冊
曲面的切平面和法線的概念142曲面法向量的概念142曲面的切平面與法線方程143曲面法向量的方向餘弦144二元函式全微分的幾何意義1458.7 方嚮導數與梯度145方嚮導數定義...
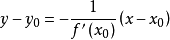



 法線
法線