基本介紹
- 中文名:泊松定理
- 外文名: Poisson theorem
- 提出者:S.D.泊松
- 套用學科:物理
- 適用領域範圍:確定地質體總磁化方向及其在分析火山岩活動
- 物理意義:重磁異常的對應分析的物理意義
分配,定理,特性,驗證,習題,
分配
[英] Poisson theorem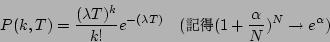
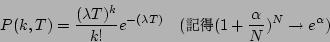
Poisson 分配
考慮下列現象:每小時服務台訪客的人數,每天家中電話的通數,一本書中每頁的錯字數,某條道路上每月發生車禍的次數,生產線上的疵品數,學生到辦公室找老師的次數……。大致上都有一些共同的特徵:在某時間區段內,平均會發生若干次「事件」,但是有時候很少,有時又異常地多,因此事件發生的次數是一個隨機變數,它所對應的機率函式稱為 Poisson 分配。
定理
特性
一個 Poisson 過程有三個基本特性:
⑴在一個短時間區間 內,發生一次事件的機率與
內,發生一次事件的機率與 成正比:
成正比: 。
。



⑵在短時間內發生兩次以上的機率可以忽略。
⑶在不重疊的時間段落里,事件各自發生的次數是獨立的。
驗證
現令 P(k,T) 表示在時間區間 T 中發生 k 次事件的機率(注意 T 表示時間區間的長度,而不是絕對時間),由⑴⑵知 ,且
,且 ,
,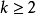 。現將 T 分割成 N 個短時間區段 (即
。現將 T 分割成 N 個短時間區段 (即 ),利用 ⑶各時間區段出現之事件是獨立的條件,可知
),利用 ⑶各時間區段出現之事件是獨立的條件,可知


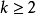

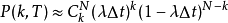


固定 k,當 時
時



習題
例題1
⑴驗證 。
。

⑵令 。求 E(X) 與 Var(X)。
。求 E(X) 與 Var(X)。

(Ans. m,m.)
例1
.一公司之電話通數大約每小時 20 通,求在 5 分鐘內一通電話也沒有的機率?每小時 20 通,表示每分鐘平均 通/分。因此在 5 分鐘的時間區間中,平均的電話通數為
通/分。因此在 5 分鐘的時間區間中,平均的電話通數為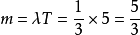 。所以
。所以

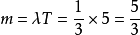
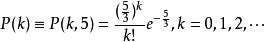

經計算這個機率分配的期望值 ,標準差
,標準差 。右圖是 P(k) 的圖形,當然由於 k= 0,1,…,所以這只是部分圖形。讀者可與一般的二項分配的圖形比較。
。右圖是 P(k) 的圖形,當然由於 k= 0,1,…,所以這只是部分圖形。讀者可與一般的二項分配的圖形比較。



例. 下表是 1910 年 Rutherford 觀察放射性物質放射 α 粒子的記錄,每次觀察 7.5秒,共觀察 2608 次。
粒子數次數頻率P(k)
0 57 0.022 0.021
1 203 0.078 0.081
2 383 0.147 0.156
3 525 0.201 0.201
4 532 0.204 0.195
5 408 0.156 0.151
6 273 0.105 0.097
7 139 0.053 0.054
8 45 0.017 0.026
9 27 0.010 0.011
≥10 16 0.006 0.007
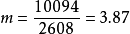
這裡 P(k)=P(k,7.5),其中 ,m=3.87(見表最末欄),為 7.5 秒中 α 粒子放射之平均個數。可以看到,如果假設 α 粒子的放射是一 Poisson 過程,結果相當吻合。
,m=3.87(見表最末欄),為 7.5 秒中 α 粒子放射之平均個數。可以看到,如果假設 α 粒子的放射是一 Poisson 過程,結果相當吻合。

例2
. 令一放射性物質在時間 t 時所含之放射性粒子總量為 N(t),如果假設放射粒子是一 Poisson 過程,則在短時間 Δt後,

注意到 是一期望值的形式。所以
是一期望值的形式。所以


這可看成輻射定律的「證明」。
對外搜尋關鍵字:
.輻射定律
指數分配與排隊理論
令 W 表示在 Poisson 過程中,由開始到第一次事件發生的時間(這是一隨機變數)。由上節知
P(W>t)=P(在[0,t]中無事件發生)
=

但

所以

讓我們討論排隊理論。排隊的現象無所不在:買各種票、吃自助餐、超商、百貨公司……等。顧客揣度「應該排那一服務櫃檯會比較快?」「到底還要排多久?」是城市生活的基本問題;相對的,商家也要盤算到底在何時要開幾個視窗櫃檯才符合成本,探討這個問題的數學理論通稱為排隊理論,而指數分配經常被用到排隊理論,當作服務客人時間(這是一隨機變數)的機率密度函式。
讓我們假設某櫃檯,服務客人的平均時間為 μ,想像在服務結束後,櫃員會亮燈請下一位客人進來,則亮燈的平均時間是 μ。若將「燈亮」視為一事件發生,則亮燈的過程近似於一 Poisson 過程。而且前面定義的 W 正好表示兩次亮燈間的間隔。所以 W 的機率密度函式是指數分配:
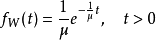
例3.
現假設一櫃檯平均服務時間為 3 分鐘,設等待時間的機率密度函式為
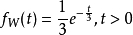
⑴等候時間超過6分鐘的機率是多少?


事實上,等候超過 T 分鐘的機率是 。
。

⑵另一個合理的問題是,如果在我前面還有另一個客人,則我怎么描述,我等待時間的機率分配呢?
令 W1 是第一個客人等待的時間,W2 是第一個客人開始被服務後,我所等待的時間,則 W1 ~ W2~ W3,而且總等待時間 U = W1+W2,另外顯然 W1 與 W2 是互相獨立的。所以我們的問題就是要計算 fU(t),由309頁例子的方法,可以計算得

或者,如果將指數分配 fW(t) 想成是 分配,則此相當於
分配,則此相當於


因此如果我們想知道總等候時間不超過 5 分鐘的機率,則



有一半的機會。
⑶如果前面有 n-1 個客人時,則可定義 U=W1+W2+ ···+ Wn,其中 Wi 彼此獨立,由 Gamma 分配性質知 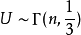 ,即
,即
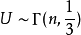
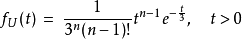
這告訴我們  分配與排隊理論的關係。我們將細節留作習題。
分配與排隊理論的關係。我們將細節留作習題。

例題2
⑴超級市場一服務員平均服務時間為 2 分鐘,若用指數分配當作等候時間之機率分配,則機率密度函式是什麼?
⑵如果他正開始服務一位客人,而你前面還有一位客人在等候,則你會等超過 6分鐘的機率是多少?
⑶若服務員甲平均服務時間為 2 分鐘,而服務員乙之平均服務時間為 3 分鐘,如果你選擇乙,你朋友選擇甲,且一起開始接受服務,則你會比朋友快的機率是多少?(當然甲與乙的服務是相互獨立的)你能給出一個一般的計算公式嗎?