殘差圖

殘差圖是指以某種殘差為縱坐標，以其他適宜的量為橫坐標的散點圖。這裡橫坐標有多種選擇，最常見的選擇是：1.因變數的擬合值；2. 某自變數的觀察值；3.在因變數的觀察值Y₁，…，Y_n為一時間序列時， 橫坐標可取為觀察時間或觀察序號。通過對殘差及殘差圖的分析，以考察模型假設的合理性的方法，稱為殘差分析。這些方法比較直觀，套用上效果也好，目前許多統計軟體包均能打出殘差圖。可用它來檢查回歸線的異常點。在分析測試中常用的散點圖是以自變數為橫坐標的殘差圖。

基本介紹

• 中文名：殘差圖
• 外文名：plot of residuals
• 所屬學科：數學
• 相關概念：殘差、回歸線、殘差分析等

定義

以殘差 為縱坐標，以擬合值 或對應的數據觀測序號或數據觀測時間為橫坐標的散點圖統稱為殘差圖。殘差圖是進行模型診斷的重要工具。

回歸值與殘差的殘差圖

為檢驗建立的多元線性回歸模型是否合適，可以通過回歸值 與殘差的散點圖來檢驗。其方法是畫出回歸值 與普通殘差的散點圖 ，或者畫出回歸值 與標準殘差的散點圖 ，其圖形可能會出現下面三種情況(如圖1所示)：

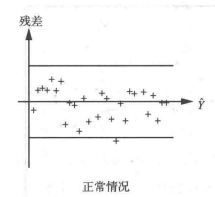圖1（a）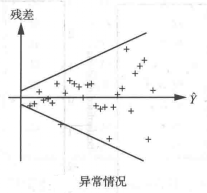

圖1（b）

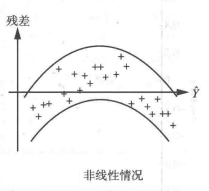圖1（c）

對於圖1(a)的情況，不論回歸值 的大小，而殘差 (或 )具有相同的分布，並滿足模型的各假設條件；對於圖1(b)的情況，表示回歸值 的大小與殘差的波動大小有關係，即等方差性的假設有問題；對於圖1(c)，表示線性模型不合適的樣本，可能有異常值存在。

對於圖1(a)，如果大部分點都落在中間(b)部分，而只有少數幾個點落在外邊，則這些點對應的樣本，可能有異常值存在。

以自變數為橫坐標的殘差圖

以每個 的各個觀測值 為點的橫坐標，即以自變數為橫坐標的殘差圖。與擬合值 為橫坐標的殘差圖一樣，滿意的殘差圖呈現圖1(a)的水平帶狀。如果圖形呈現圖1(b)的形狀，則說明誤差是等方差的假設不合適。若呈現圖1(c)的形狀，則需要在模型中添加 的高次項，或者對 作變換。

殘差的QQ圖

設 是殘差 的次序統計量，，令

其中，為標準常態分配的分布函式，為反函式。稱為的期望值。

可以證明，若是來自常態分配總體的樣本，則點應在一條直線上。因此，若殘差的正態QQ圖中的點的大致趨勢明顯地不在一條直線上，則有理由懷疑對誤差的正態性假設的合理性；否則可認為誤差的正態性假設是合理的。

殘差個案排序圖

在MATLAB中，還可以通過rcoplot()函式畫出殘差個案排序圖形，以此來判斷樣本是否為異常值樣本，其使用格式為：rcoplot(r，rint)。

其中，參數r為回歸殘差，rint為殘差的預測區間。