偏殘差圖

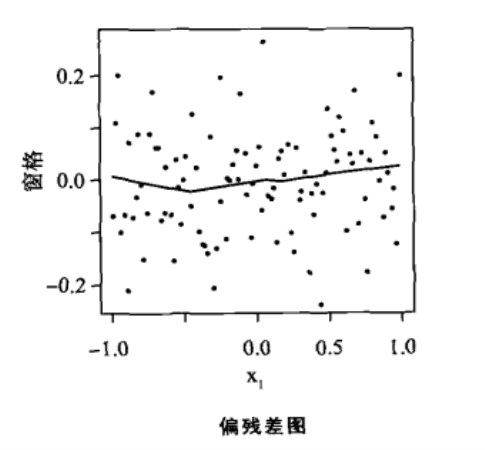
偏殘差圖(Partial Residual Plot)是多元回歸中常用的診斷工具，特別是評估模型中在一個或另一個解釋變數中是否包含非線性項。在多元回歸y=β₀+β₁x₁+…+β_px_p+ε中，若欲反映其中變數X_j與因變數y之間的關係並用圖形顯示，其方法之一是用偏殘差圖。偏殘差圖是用偏殘差代替殘差圖中的普通殘差。

基本介紹

• 中文名：偏殘差圖
• 外文名：Partial Residual Plot
• 所屬學科：數學（數理統計）
• 簡介：多元回歸中常用的診斷工具
• 特點：用偏殘差代替殘差圖中的普通殘差
• 相關概念：偏殘差，散點圖等

基本介紹

偏殘差圖由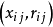的散點圖組成，其中，是關於第i個解釋變數的第j次觀察，定義為：

其中，是反應變數的均值，是第i個解釋變數的均值，是關於解釋變數i的回歸係數的估計，是第j次觀察的殘差。圖形中的非線性表明回歸模型中包含中的非線性項。

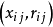
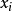
偏殘差圖是用偏殘差代替殘差圖中的普通殘差。

相關分析

假設y是可加地但並非必然線性地相關於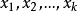 ，則有：

若偏回歸函式 是簡單而單調的，那我們就能通過套用凸出法則來找到能使y和預測變數 關係線性化的變換。在另一種情況下，若 為 的簡單多項式形式，比如二次或三次多項式，那么我們就可以指定一個包含預測變數多項式形式的參數模型。

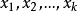
由於預測變數之間的相關性，在多元回歸中尋找非線性關係要比在簡單回歸中更困難。因此，雖然y關於 散點圖能夠提供關於兩個變數之間邊際關係的信息，但它並不必然能告訴我們在控制其他xs不變的情況下y與 之間的偏關係 。

在大多數場合下，偏殘差圖(也被稱做成分+殘差圖，component+residual plots)能夠幫助檢測多元回歸中的非線性。讓我們擬合一個初步的線性最小二乘回歸：

此時為了得到 的偏殘差，我們向關於y與 之間關係的

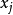
線性成分中加入最小二乘法殘差：

這裡關鍵的想法是y與 之間未進入模型的非線性關係應能體現在最小二乘法的殘差中，從而通過描繪並平滑 與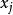 的關係能夠揭示y與 之間的偏相關關係。我們將平滑後的偏殘差圖看做對偏回歸函式的估計值 。我們對每一個預測變數 重複這一過程。

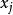
基於加拿大職業聲望數據職業聲望對收入和教育回歸的偏殘差圖如圖1所示。每一幅圖中的實線給出了局部線性擬合；虛線給出了最小二乘法擬合結果並描繪了從相應預測變數方向上側面看過去的多元最小二乘回歸平面。

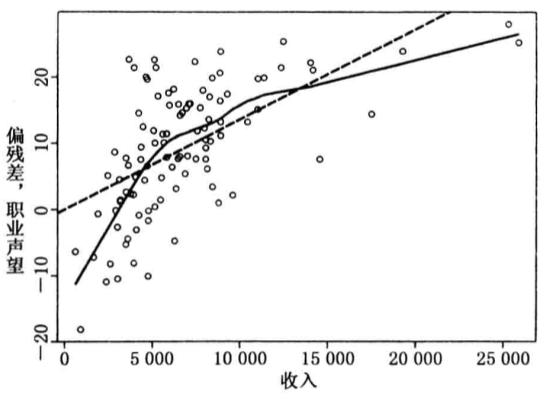圖1（a）

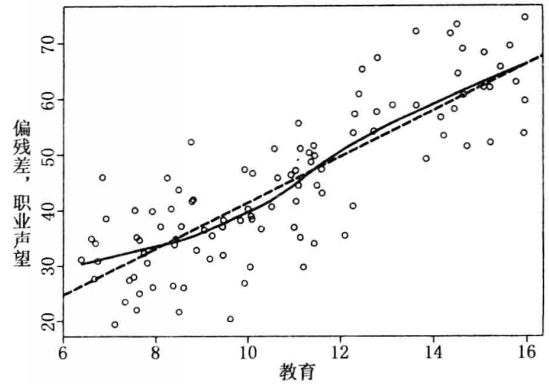圖1（b）

圖1 關於職業聲望對(a)收入(b)教育回歸的偏殘差圖。每一幅圖中繪出使用跨距=0.6的局部線性擬合，以及線性最小二乘線。

從圖1(a)中可以明顯地看到控制教育後聲望和收入的關係明顯是非線性的。雖然非參數回歸曲線並不完全平滑，凸起部分指向上方和左方，提示我們要沿冪階和根式階向下變換收入變數。視覺試錯法表明對收入的對數變換能夠將聲望與收入的關係拉直。除非所有的偏殘差圖部呈現相似的模式，我們在多元回歸中更喜歡變換預測變數而不是回響變數，這是由於對y的變換將會改變它與所有x之間的關係。

·圖1(b)暗示聲望與教育之間的偏關係是非線性、單調、非簡單的。其結果是，對教育的冪變換並不可取。我們可以嘗試對教育使用立方回歸(即，在回歸模型中引入包括教育、教育的平方和教育的立方)，但由於偏離線性較小，另一個可行方案是直接將教育的影響當做線性的。

對職業聲望關於教育和收入對數(以2為底數)進行回歸可得到如下結果：

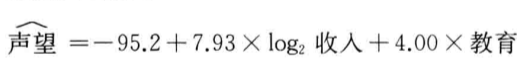
因此，保持教育不變，收入翻倍(即增加1單位的log₂收入)平均起來能夠使職業聲望增加大約8點；保持收入不變而增加1年教育則平均能使聲望增加4點。