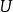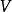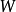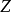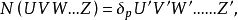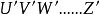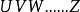基本介紹
概念,基本原理,
概念
量子力學中,算符乘積是與順序有關的,例如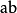 不一定等於
不一定等於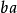 。而正規乘積指這樣一種特定的乘積順序:在乘積中,所有的消滅算符都在產生算符的右邊。常常用
。而正規乘積指這樣一種特定的乘積順序:在乘積中,所有的消滅算符都在產生算符的右邊。常常用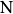 表示正規乘積,例如
表示正規乘積,例如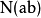 當
當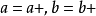 時,
時,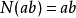 。當
。當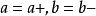 時,
時, 。其中
。其中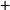 表示消滅,
表示消滅, 表示產生。對於費米子,改變算符順序應添加額外的負號。
表示產生。對於費米子,改變算符順序應添加額外的負號。
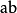
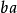
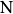
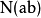
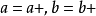
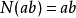
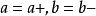

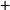

由於正規乘積所有消滅算符都在產生算符右邊,因此正規乘積的真空期望總是0。因此,常常用wick收縮的辦法,將編時乘積化為一系列正規乘積和更小的編時乘積以化簡運動方程。
基本原理
若在算符的乘積中,所有代表粒子湮沒的算符都排在右邊,所有代表粒子產生的算符都排在左邊,則這種算符稱為正規乘積。通常用符號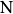 來表示。將任意次序的算符乘積排列稱為正規乘積的操作。
來表示。將任意次序的算符乘積排列稱為正規乘積的操作。
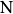
例如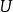 、
、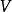 、
、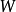 、
、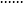 、
、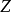 是一系列的產生算符和湮沒算符,正規乘積為:
是一系列的產生算符和湮沒算符,正規乘積為: