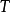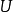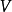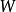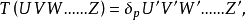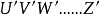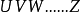量子力學中，算符的乘積是與順序有關的，例如ab和ba就不一定相等。而編時乘積是指時間相關的算符相乘，順序按照時間排列這樣一種特殊的算符乘積。
基本介紹
- 中文名：編時乘積
- 外文名：Time Order
- 相關：量子力學或量子場論
- 類別：符合算符定義
- 定義：時間相關的算符相乘
- 套用學科：量子力學術語
定義,基本原理,
定義
量子力學中，算符的乘積是與順序有關的，例如ab和ba就不一定相等。而編時乘積是指時間相關的算符相乘，順序按照時間排列這樣一種特殊的算符乘積。常用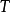
表示，例如當
，
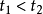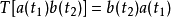，當
，
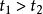，即從右往左時間是遞增的。在很多情況下，等時算符往往是對易的，因此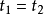
時順序不重要。一般不會使用等時不對易的算符的編時乘積。
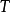
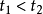
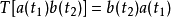
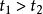
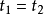
在相互作用表象中，量子態所滿足的運動方程為相互作用哈密頓量的一系列編時乘積的積分。量子場論中，兩個場量的編時乘積的真空期望值等於傳播子。
把編時乘積轉化為一系列正規乘積和更小的編時乘積之和的做法就叫做wick收縮。由於正規乘積的真空期望為零，這種做法常用於將編時乘積化為一系列傳播子的乘積的積分之和。
基本原理
場的相互作用是用相互作用哈密頓密度
來表征的。中常含有不同場的場算符的連乘積。每一個場算符又是一系列粒子的產生算符和湮沒算符之和，而且這些算符都是時間的函式。在乘積中，算符的排列次序對計算有重要作用。
在算符的連乘積中，若各算符是按時間次序排列的，即對應於較早時間的算符在右邊，對應於較遲時間的算符在左邊，則這種算符的乘積稱為編時乘積。通常用符號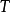來表示將任意次序的算符乘積改變為編時乘積的操作。例如
、
、
、
、
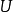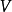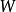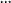是一系列的算符，都是時間的函式，編時乘積為：
