正十二面體

正十二面體是由12個正五邊形所組成的正多面體，它共有20個頂點、30條棱、160條對角線，被施萊夫利符號{5,3}所表示，與正二十面體互成對偶。它是一種只具有正四面體對稱性的五角十二面體的特殊形式，五角十二面體的另一種特殊形式是具有正八面體對稱性的卡塔蘭多面體菱形十二面體，它（加上所有其它的五角十二面體）都與正十二面體在拓撲上等價。正十二面體還是截頂五方偏方面體的特例。其四維類比為正一百二十胞體。

基本介紹

• 中文名：正十二面體
• 外文名：Pentagonal dodecahedron
• 性質：五個柏拉圖立體之一
• 又稱：正五角十二面體
• 套用學科：幾何學
• 定義：由12個正五邊形所組成的正多面體

性質

面的圖形：正五邊形

面的數目：12
邊的數目：30
頂點數目：20
二面角角度：如果正十二面體棱長為a：
表面積：

體積：

外接球半徑：

內切球半徑：

中交球半徑：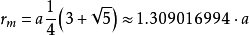

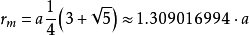
• 我們亦可以將上述三式寫作：

外接球半徑：

內切球半徑：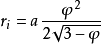

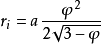
中交球半徑：

（在這裡φ是黃金分割數，φ=）

注意到棱長為a的正十二面體的外接球同樣外接於棱長為φa的立方體，並且其內切球半徑（也即面心距）等於棱長為φa的正五邊形的邊心距。

對偶多面體：正二十面體

坐標系

如果我們以正十二面體的形心為原點建立三維直角坐標系，那么其20個頂點可被描述為：

(0,±φ,±1/φ)
(±1/φ,0,±φ)
(±φ,±1/φ,0)
(±1,±1,±1)
其中φ = (1+√5)/2，是黃金分割數，也被寫作τ，約等於1.618。
該正十二面體棱長為/_φ=√5–1。其內接球半徑正好為√3。

頂點坐標：
	橙色的頂點位於(±1, ±1, ±1)，形成了其一個內接立方體(虛線所示)。
	綠色的頂點位於(0, ±φ, ±1/φ)，形成了y–z平面上的一個黃金矩形。
	藍色的頂點位於(±1/φ, 0, ±φ)，形成了x–z平面上的一個黃金矩形。
	粉色的頂點位於(±φ, ±1/φ, 0)，形成了x–y平面上的一個黃金矩形。
相鄰頂點間的距離是2/φ，頂點到原點的距離是√3.; φ= (1 + √5) / 2是黃金分割數。

幾何關聯

• 正十二面體是一個無窮家族——截頂偏方面體的第3個成員（截頂五偏方面體）。這類多面體可以被看作是將偏方面體在旋轉對稱軸上的兩個相對的頂點截去而成。
• 正十二面體的星形化體構成了4個星形正多面體中的3個。
• 我們可以在正十二面體的20個頂點中選取5組這樣的頂點，使任意兩個頂點的連線都是正十二面體正五邊形面的一條對角線，這樣能構成正十二面體的內接立方體，5個內接立方體一起構成了——複合多面體——五複合立方體；我們還可以進一步對內接立方體做交錯操作，得到正十二面體的內接正四面體，如果我們只在內接立方體中取一個正四面體，則5個正四面體構成了有手征性的複合多面體——五複合四面體；如果取兩個，則10個正四面體構成了複合多面體——十複合四面體，這三個複合多面體都是正十二面體的小面化體。
• 正十二面體的完全對稱群是正二十面體對稱群I_h，考克斯特群[5,3]，群階120，還有一個抽象群結構A₅×Z₂。
• 當正十二面體和正二十面體內接於同一球時，儘管正二十面體有更多的面，但正十二面體占據球的體積（66.49%）要多於正二十面體占據的球的體積（60.54%），這一點與二維不同。
• 棱長相同為1的正十二面體的體積（7.663...）是正二十面體體積（2.181...）的三倍半多。

相關數學問題

• 哈密頓路徑的理論就是源自一個和正十二面體有關的問題：試求一條路徑，沿正十二面體的棱經過它所有的頂點。

真實世界

• 因為一年有12個月，正十二面體正好用來製作月曆。
• Pariacoto virus的形狀結構是正十二面體。
• 在英國到匈牙利，至到義大利東部等地，找到過百個形狀接近十二面體、以銅或石頭製造的空心物件。它們被稱為Dodecaeder，用途不明。
• 五魔方（Megaminx）就是正十二面體製作出來的魔方。

化學：

• 硫化鐵結晶體有時會出現接近正十二面體的形狀。
• 最小的富勒烯C₂₀結構如正十二面體。
• 正十二面體烷C₂₀H₂₀是個人工合成的碳氫化合物。