基本介紹
- 中文名:正交變換群
- 外文名:orthogonal transformation group
- 所屬學科:數學
- 所屬問題:高等幾何(幾何基礎)
- 別稱:運動群或度量群
- 簡稱:正交群
- 簡介:全體正交變換所構成的變換群
基本介紹
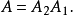

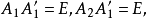

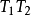
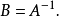



正交變換群的幾何—歐氏幾何
相關概念

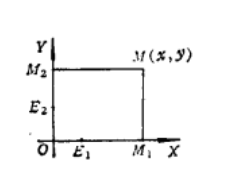 圖1
圖1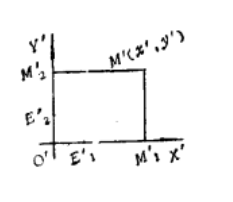 圖2
圖2

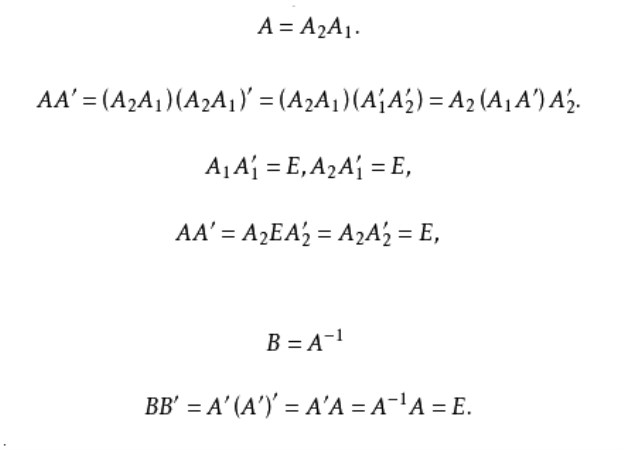
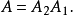

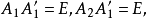

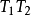
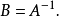




 圖1
圖1 圖2
圖2

正交變換群(orthogonal transformation group)亦稱運動群或度量群,簡稱正交群,是一類基本的變換群,即全體正交變換所構成的變換群。例如,平面上全體正交變換的集合構成...
正交群是一類重要的典型群。在實數域的特殊情形,全體n×n正交方陣在矩陣乘法下構成的群稱為n次正交群,記為O(n)。一般地,設V是域K上n維列向量空間,Q(x)=...
變換群是幾何學研究的重要對象。即由變換構成的群。設G是集合S的一一變換所構成的集合,若它滿足:1.集合內任二變換之積仍屬於這集合;2.集合內任一變換的逆變換...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。仿射變換群是指仿射空間A的所有自同構組成A的置換群的子群,稱為A的...
由有限次中心射影的積定義的兩條直線間的一一對應變換稱為一維射影變換。由有限次中心射影的積定義的兩個平面之間的一一對應變換稱為二維射影變換。因為正交變換...
正交表示是正交變換的推廣。有限群在實數域上的任意的矩陣表示都等價於一個正交表示。...
1 正交變換 2 逆變換 平移變換正交變換 編輯 .平移是第一種正交變換.例如在平面...所有平移變換的全體構成一個群,稱為平移群.平移變換的概念可以推廣到n維歐氏空...
(X,t)→(GX,t),其中G:R3→ R3為某正交變換。作為一個李群,伽利略變換的維度為10。伽利略變換變換的局限 編輯 伽利略變換與牛頓的絕對時間、絕對空間的概念有...
空間旋轉變換(rotation transformation in space)是一種特殊的幾何變換,指空間的所有點繞同一直線旋轉同一角度的變換,亦稱特徵正交變換,是一種特殊的正交變換,n維...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。運動群亦稱正交變換群或度量群。簡稱正交群。一類基本的變換群。即全體...
2.集合內任一變換的逆變換仍屬於這集合,則稱G為S的一個變換群。例如,平面上正交變換的全體構成的變換群稱為正交群;平面上仿射變換的全體構成的變換群稱為仿射...
對稱操作群:由物體的對稱操作構成的群。對稱操作:物體在正交變換(保持兩點間距離不變的幾何操作,如旋轉,反伸,反映)下不變,則該變換為物體的對稱操作。...
