歐拉猜想

歐拉猜想是歐拉提出的對費馬最後定理引出的猜想，歐拉猜想每個大於2的整數n，任何n- 1個正整數的n次冪的和都不是某正整數的n次冪，1966年L. J. Lander和T. R. Parkin推翻了這一猜想。

提出

歐拉猜想是由歐拉提出，從費馬最後定理引出的猜想。這猜想是說對每個大於2的整數n，任何n- 1個正整數的n次冪的和都不是某正整數的n次冪，也就是說以下不定方程無正整數解。

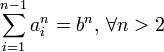
推翻

這猜想在1966年被L. J. Lander和T. R. Parkin推翻。他們找出n= 5的反例：

27^5+ 84^5+ 110^5+ 133^5= 144^5

1988年，Noam Elkies找出一個對n= 4製造反例的方法。他給出的反例中最小的如下：

2682440^4+ 15365639^4+ 18796760^4= 20615673^4

Roger Frye以Elkies的技巧用電腦直接搜尋，找出n= 4時最小的反例：

95800^4+ 217519^4+ 414560^4= 422481^4

現在仍未知道當n> 5時的反例。