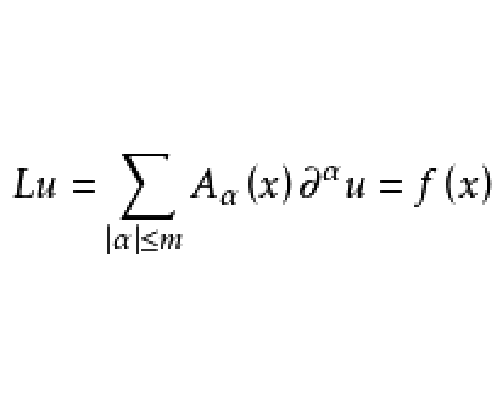次特徵帶

次特徵帶(bicharacteristic strip)又名雙特徵帶，是偏微分方程理論中的一個概念。對於一般的m階線性偏微分運算元P(x，D_x) ，這裡P(x，D_x)是的多項式，其象徵為P(x，ξ)，主象徵為P_m(x，ξ)。為了方便，記t為x₀，x= (x₀，x₁，...，x_n)相應於以上結果是：對於超曲面有如果一個超曲面φ(x)=0(grad φ≠0)適合，則稱它是P的特徵超曲面。如果在(x，ξ)空間考慮，並視ξ為一向量，(x，ξ)就成為x空間中x點處的接觸元素。這樣，其解將稱為P的次特徵帶，它在x空間的投影稱為次特徵曲線。一切適合於一定條件的特徵超曲面都是由次特徵曲線“織”成的。

基本介紹

• 中文名：次特徵帶
• 外文名：bicharacteristic strip
• 所屬學科：數學
• 屬性：偏微分方程理論中的一個概念
• 相關概念：特徵，特徵帶，微局部分析等
• 類型：數學名詞

基本介紹

次特徵是偏微分方程理論中的一個重要概念，設是一個方程(組)的特徵曲面，可以證明S可嵌入該方程(組)的一族特徵曲面，其中c為常數，這樣就是一個一階偏微分方程的解。例如，對於m階線性偏微分方程

其中為n重指標，應滿足一階偏微分方程

做為(2)的積分曲面由它的n-1參數的特徵帶族織成。可以證明(1)的特徵曲面由(2)的n-2參數的特徵帶族織成，我們把織成S的特徵帶和特徵曲線分別稱為(1)的次特徵帶和次特徵曲線。由此我們可不藉助於特徵曲面直接定義(1)的次特徵，由(2)考慮函式

其中作關於的Hamilton-Jacobi方程組

(4)的一個解，若滿足

則稱其為(1)的次特徵帶，次特徵帶在空間的投影稱為(1)的次特徵曲線。

相關概念

特徵(曲線)

特徵(characteristics)是特證曲面的簡稱，對於偏微分方程理論的研究起著非常重要的作用，例如，對於一個m階線性偏微分方程(1)，它的主部為

其中為n重指標，對於任意的，向量稱為L在點的一個特徵方向，如果

其中，顯然在的所有特徵方向組成一個以為頂點的m次錐面，通常稱為L在的法線錐，一個光滑曲面S如果其上每一點的法線方向都是L在該點的特徵方向，則S稱為L的特徵曲面，若S可用方程表示，其中且，則S為特徵曲面在S上成立。又如對一階線性方程組

其中，u為m維未知函式向量，為已給的m維函式向量，和均為已給的m階函式方陣，對於，向量稱為(5)在的特徵方向，如果

若曲面，其中且使褥

在S上處處成立，則稱S是(5)的特徵曲面，一般高階線性方程組的特徵可類似定義，對於線性方程(組)，顯然它的特徵僅與該方程(組)的主部有關，對於非線性方程(組)可以利用將其線性化的方法定義特徵概念，此時特徵不僅依賴於方程，而且還依賴於未知函式。

哈密頓-雅可比方程

哈密頓-雅可比方程(Hamilton-Jacobi equation)是不含未知函式本身的一階非線性方程的特徵微分方程組，在分析力學、幾何學、變分學，特別是偏微分方程的特徵理論中常常遇到不顯含未知函式本身的一階非線性偏微分方程

寫其特徵微分方程組時，可以獨立地列出關於x，p的導數的方程：

(7)稱為函式F或方程F=0的哈密頓-雅可比方程，(7)稱為哈密頓方程組或典則方程組，(7)的解x_i=x_i(s)，p_i=p_i(s)(i=1，2，…，n)滿足方程(6)時稱為函式F(x，p)的雙特徵帶，而x_i=x_i(s)稱為雙特徵曲線或簡稱雙特徵(有時也稱為次特徵)。如果F(x，p)是p的齊次函式，則使得F(x₁(s)，(x₂(s)，…，x_n(s)，p₁(s)，p₂(s)，…，p_n(s))≡0的雙特徵帶稱為零雙特徵帶，一階偏微分方程的標準型也稱為哈密頓-雅可比方程(參見“光程函式方程”)。