梅涅勞斯逆定理是若有三點F、D、E分別在邊三角形的三邊AB、BC、CA或其延長線上,且滿足AF/FB×BD/DC×CE/EA=1,則F、D、E三點共線。利用這個逆定理,可以判斷三點共線。
基本介紹
- 中文名:梅涅勞斯逆定理
- 類型:定理
- 領域:幾何
- 滿足:AF/FB×BD/DC×CE/EA=1
定理
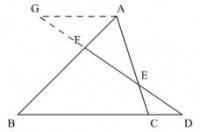
梅涅勞斯逆定理是若有三點F、D、E分別在邊三角形的三邊AB、BC、CA或其延長線上,且滿足AF/FB×BD/DC×CE/EA=1,則F、D、E三點共線。利用這個逆定理,可以判斷三點共線。

梅涅勞斯逆定理是若有三點F、D、E分別在邊三角形的三邊AB、BC、CA或其延長線上,且滿足AF/FB×BD/DC×CE/EA=1,則F、D、E三點共線。利用這個逆定理,可以...
梅涅勞斯(Menelaus)定理(簡稱梅氏定理)最早出現在由古希臘數學家梅涅勞斯的著作《球面學》(Sphaerica)中。任何一條直線截三角形的各邊或其延長線,都使得三條不相鄰...
梅涅勞斯逆定理常用來證明三點共線問題,如:笛沙格定理,帕斯卡定理,蝴蝶定理都可用梅涅勞斯定理來證明。 ...
梅涅勞斯(Menelaus),提出了梅涅勞斯定理。他指出:如果一條直線與△ABC的三邊AB、BC、CA或其延長線交於F、D、E點,那么AF/FB×BD/DC×CE/EA=1。...
用梅涅勞斯定理及面積法的觀點來看,這個結論是較為容易證明的,只需要善用圓冪定理帶來的相似即可。結論6:列出圓內三線共點的塞瓦定理逆定理,之後利用圓冪定理帶來...
我們決定將證明清宮定理的方針確定如下:因為D、E、F三點中,有兩點在△ABC的邊上,其餘一點在邊的延長線上,如證明,則根據梅涅勞斯定理的逆定理,就可證明DEF三點...
由梅涅勞斯定理的逆定理知:L,M,N三點共線證畢故牛頓定理1成立牛頓定理定理2 編輯 圓外切四邊形的兩條對角線的中點,及該圓的圓心,三點共線。...
又梅涅勞斯定理的逆定理知,PQR三點共線。得證勒莫恩線拓展 編輯 事實上,勒莫恩線是帕斯卡線的一個特例,當圓內接六邊形退化為三角形時,帕斯卡線即為勒莫恩線。...
因L、M、N三點分別在△PQR三邊或其延長線上,敵由梅涅勞斯定理的逆定理知,L、M、N三點共線。共點圓共點 編輯 有幾個圓交會於一點時,這些圓叫做共點的圓...
24.梅涅勞斯定理的逆定理:(略)25.梅涅勞斯定理的套用定理1:設△ABC的∠A的外角平分線交邊CA於Q、∠C的平分線交邊AB於R,、∠B的平分線交邊CA於Q,則P、Q...
梅涅勞斯定理托勒密定理西姆松線的存在性及性質。賽瓦定理及其逆定理。1981年,中國數學會開始舉辦“全國高中數學聯賽”,經過1981、1982、1983三年的實踐,這一民眾性的...
