朗之萬方程,布朗粒子運動方程的一般形式。
基本介紹
- 中文名:朗之萬方程
- 外文名:Langevin’s equation
- 簡介:布朗粒子運動方程的一般形式
- 對象:粒子
- 別稱:愛因斯坦關係
朗之萬方程
正文
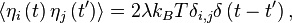 力η(t)具有高斯機率分布與自協方差函式
力η(t)具有高斯機率分布與自協方差函式朗之萬方程,布朗粒子運動方程的一般形式。
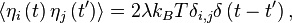 力η(t)具有高斯機率分布與自協方差函式
力η(t)具有高斯機率分布與自協方差函式在統計物理中, 朗之萬公式(保羅·朗之萬,1908年) 是一個描述自由度的子集的時間演化的隨機微分方程。 這些自由度,通常是那些在與系統的其他(微觀的)變數相比,...
保羅·朗之萬(Paul Langevin,1872年1月23日-1946年12月19日)法國物理學家。主要貢獻有朗之萬動力學及朗之萬方程。 Langevin在民國時期的資料中常譯為郎之萬 ...
一個受隨機力的經典粒子,經由朗之萬方程(Langevin equation)可以得到福克-普朗克方程。另外再藉由福克-普朗克方程也可推導薛丁格方程。 [1] ...
朗之萬方程式可推廣為下述形式(1)式中是時間的周期函式,摩擦阻力由粒子瞬時速度決定,但有滯後效應,γ(t)為滯後阻力函式。 布朗粒子受到外力作用時,感應的平均速度...
從輻射與原子的全量子理論出發導出朗之萬方程、福克—普朗克方程、密度矩陣方程。下面是典型的關於輻射的湮沒與產生算符b、b+的朗之萬方程。
朗之萬方程的數值模擬及其策略、主方程的蒙特卡羅模擬、反常擴散的數值模擬方法、相變模型的隨機模擬;第二部分為量子耗散系統,包含第10-15章,內容包括路徑積分的基本...
在統計物理中的郎之萬方程,應該是隨機微分方程,而且不是普通意義下的隨機微分方程代表布朗粒子所受到的隨機力,它被視為一個白噪音過程。由於白噪音不是一個普通...
3.7朗之萬方程:布朗運動的特點653.8kushner直接平均法663.9國小習率參數下統計lms學習理論673.10計算機實驗Ⅰ:線性預測683.11計算機實驗Ⅱ:模式分類69...
第2章和第3章分別介紹了當今研究隨機動力學的主要手段:朗之萬方程和福克一普朗克方程。著重討論了求解這兩種方程的方法及其導出的結論。第4章論述了隨機行為之源—...
其內容包括隨機變數和機率分布、演化方程、反常擴散現象、非各態歷經隨機運動、含非歐姆摩擦的廣義朗之萬方程、連續時間無規行走、分數階微積分、分數階朗之萬方程...
演化方程的主要形式有主方程、有效朗之萬方程、福克-普朗克方程和廣義京茨堡-朗道方程等。 [4] 協同學學科內容 編輯 協同學的主要內容就是用演化方程來研究協同...
8.1朗之萬方程8.1.1朗之萬方程8.1.2隨機變數的機率分布8.1.3愛因斯坦關係8.2福克爾普朗克方程8.2.1隨機過程的機率描述8.2.2福克爾-普朗克方程...
附錄F 非平衡熱力學的朗之萬方程 附錄G 旋轉和映射 附錄H 複數維薩特分布 術語 參考文獻 建議閱讀文獻 中英文術語對照表 [1] 詞條圖冊 更多圖冊 參考...
2.2 朗之萬方程 2.3 福克-普朗克方程 2.4 具有細緻平衡的系統的福克-普朗克方程的嚴格定態解 2.5 路徑積分 2.6 複雜性的約簡·序參量·伺服原理 2.7 非平衡...
§3.5 量子朗之萬方程及真空場漲落的作用 §3.6 超螢光拍 參考文獻 索引 [1] 詞條圖冊 更多圖冊 參考資料 1. 共振螢光與超螢光 .科學文庫[引用日期2020-08-...
前10章簡潔地歸納了生命科學中用得著的核心概念,它們分別是熵、麥克斯韋ˉ玻爾茲曼分布、自由能、化學勢、相變、相變動力學、關聯函式、隨機過程和朗之萬方程。第11...
二是光場的相干態和擠壓相干態,光場的量子統計描述,光學測量與光場的相關函式,原子和光場與庫的作用,耗散與漲落的量子統計理論(主方程和量子朗之萬方程),雷射...
更為重要的是,《現代統計力學導論》討論了時間關聯函式(包括漲落一耗散定理以及朗之萬方程)、重正化群理論、蒙特卡羅模擬、液體結構等專題中的一些基本原理和基本...
3.8.3橋接法多尺度框架及廣義朗之萬方程3.8.4數值例題3.8.5對橋接法的簡短評論3.9幾種模型界面不協調性的比較參考文獻第4章廣義質點動力學多尺度模擬方法...
第五章講述漲落和動力學行為,重點是漲落的關聯特性、布朗運動、朗之萬方程和線性回響理論。各章末尾都安排一定數量的習題,習題解答可通過http://www.worldscibooks...
(1)給出多尺度分解湍流運動的方法,利用實測資料指出大氣湍流中存在多尺度過程。同時建立了多尺度朗之萬方程,從理論解釋了多尺度相關過程。
