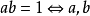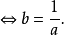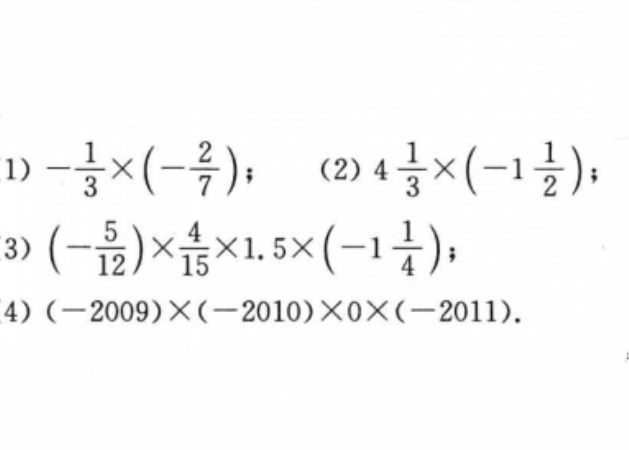有理數乘法(rule of multiplication of rational numbers)是有理數的基本運算之一。給定兩個有理數，按下面的規則得出一個新的有理數，稱為它們的積，這種運算稱為有理數乘法。其法則如下：1.兩個正有理數相乘：1) 當兩個有理數用分數形式表示時，可利用算術中分數的運算法則進行運算：(a/b)·(c/d)=ac/bd,(b≠0,d≠0)；2) 當兩個有理數用小數的形式表示時，可利用算術中小數的乘法運算法則完成，但要注意無限循環小數應化成分數來計算；3) 當兩個有理數用不同形式給出時，要首先化成同一形式，然後再按上述1)，2)運算。2.任何數同零相乘都等於零，即a·0=0·a=0。3.兩個負有理數相乘得正有理數，以它們的絕對值的積作為積的絕對值。4.正有理數乘負有理數得負有理數，以它們的絕對值的積作為積的絕對值。以上四條規則通常稱為有理數的乘法法則。
基本介紹
- 中文名：有理數乘法
- 外文名：rule of multiplication of rational numbers
- 所屬學科：數學
- 所屬問題：初等代數(有理數)
- 簡介：有理數的基本運算之一
有理數乘法的意義,有理數乘法的法則,兩個有理數相乘的方法步驟,相關說明,互為倒數的概念,
有理數乘法的意義
乘法是指具有相同加數的加法的簡便運算，引入負數後，乘法的意義沒有改變。
有理數乘法的法則
其法則如下：
(1) 兩數相乘，同號得正，異號得負，並把絕對值相乘；
(2) 任何數同0相乘，都得0；
(3) 幾個不等於0的數相乘，積的符號由負因數的個數決定，當負因數有奇數個時，積為負;當負因數有偶數個時，積為正；
(4) 幾個數相乘，有一個因數為0時，積為0。
a·b=b·a；
(a·b)·c=a·(b·c)；
(a+b)·c=a·c+b·c.
兩個有理數相乘的方法步驟
有理數乘法與有理數加法運算步驟一樣，第一 步：確定結果符號；第二步：確定結果的絕對值。
有理數乘法由於絕對值總是正數或零，因此絕對值相乘就是算術中的乘法，由此可見，有理數乘法，實質上是通過符號法則，歸結為算術的乘法來完成的。
相關說明
(1)有理數乘法法則中“同號得正，異號得負”是專指“兩數相乘”而言的，不能與加法法則相混淆。
(2)當乘數中有負號時，必須用括弧括起來，第一個因數有負號時可省略括弧，如(﹣3)×(﹣5)可寫成﹣3×(-﹣5)，但不能寫成﹣3×﹣5；
(3)任何數同1相乘仍得原數，任何數同﹣1相乘得原數的相反數。
互為倒數的概念
乘積為1的兩個數互為倒數，用式子表示為
(其中a≠0)，即若a是不等於0的有理數，則a的倒數是
，於是有
(1)0沒有倒數，而且任何一個非零數的倒數也不可能為0；
(2)倒數是它本身的數只有1和﹣1；
(3)倒數的求法：
①求一個整數(0除外)的倒數直接寫成這個數分之一即可；
②求一個真分數的倒數把這個數的分子，分母交換位置即可；
③求一帶分數的倒數，首先將它化成假分數，然後再交換分子，分母的位置；
④求一個小數的倒數，常把小數化為分數後，求其倒數。
