由兩個元素a和b按一定的順序排列成的二元組叫做有序對(或有序偶),記作(a,b)其中a稱為第一元素,b稱為第二元素。有序對可以表示有一定次序關係成對出現的事物,如平面直角坐標系中點的坐標就是有序對,(1,2)、(2,1)、(3,3)、(0,-1)都代表平面直角坐標系中不同的點。在有序對中兩個元素的次序是十分重要的。
基本介紹
- 中文名:有序對
- 外文名:ordered pair
- 別名:有序偶
- 寫為:經常寫為(a, b)
- 相關概念:有序n元組
定義



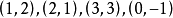
有序對的特點
有序n元組






由兩個元素a和b按一定的順序排列成的二元組叫做有序對(或有序偶),記作(a,b)其中a稱為第一元素,b稱為第二元素。有序對可以表示有一定次序關係成對出現的事物,如平面直角坐標系中點的坐標就是有序對,(1,2)、(2,1)、(3,3)、(0,-1)都代表平面直角坐標系中不同的點。在有序對中兩個元素的次序是十分重要的。



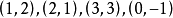




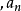
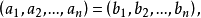

由兩個元素a和b按一定的順序排列成的二元組叫做有序對(或有序偶),記作(a,b)其中a稱為第一元素,b稱為第二元素。有序對可以表示有一定次序關係成對出現的...
有序對集合就是指由有序對構成的集合,而有序對是指從集合A、B各取一個元素a、b按順序排列構成(a,b),那么這個(a,b)就稱為一個有序對,其中a為第一元素...
有序數對,數學術語,是指用含有兩個數的詞表示一個確定的位置,其中各個數表示不同的含義,我們把這種有順序的兩個數a與b組成的數對,叫做有序數對(ordered ...
物質的系統結構或運動是確定的、有規則的。序是事物的結構形式,指事物或系統組成諸要素之間的相互聯繫。有序的相對性是指事物的組成要素的相互聯繫處於永恆的運動...
合金(以下以FeAl為例)中異類原子之間的結台力大於同類原子之間的結合力時,就趨向形成有序結構。有序化過程實質上是原子從無序排列向有序排列的轉變過程。在B2型...
笛卡爾乘積是指在數學中,兩個集合X和Y的笛卡尓積(Cartesian product),又稱直積,表示為X × Y,第一個對象是X的成員而第二個對象是Y的所有可能有序對的其中...
用有序對(α,p)表示這樣的元素。函式(b,q)稱為(α,p)的直接開拓,如果b在(α,p)的收斂圓內,在b的鄰域內p(z)=q(z)。在平面上給定一弧у(t),0≤t...
我們可以叫這個集合A為x和y的對(或無序對),並表示為{x,y}。所以這個公理的本質是:任何兩個集合都有一個對。{x,x}簡寫為{x},叫做包含x的單元素集合。...
