最小元素

最小元素法是找出運價表中最小的元素，在運量表內對應的格填入允許取得的最大數，若某行(列)的產量(銷量)已滿足，則把運價表中該運價所在行(列)划去；找出未划去的運價中的最小數值，按此辦法進行下去，直至得到一個基本可行解的方法。

基本介紹

• 中文名：最小元素
• 外文名：The smallest element
• 領域：運籌學
• 屬性：運價表中最小的元素
• 方法：從單位運價最小運價確定供銷關係
• 相關名詞：最小元素法

最小元素法是找出運價表中最小的元素，在運量表內對應的格填入允許取得的最大數，若某行(列)的產量(銷量)已滿足，則把運價表中該運價所在行(列)划去；找出未划去的運價中的最小數值，按此辦法進行下去，直至得到一個基本可行解的方法。

註：套用西北角法和最小元素法，每次填完數，都只划去一行或一列，只有最後一個元素例外（同時划去一行和一列）。當填愉殼店上一個數後行、列同時被滿足（也就是出現退化現象）時，也只任意划去一行（列）。需要填入“0”的位置不能任意確定，而要根據規則來確定。

所謂退化現象是指：當在平衡表中某一處填入一數字後，該數字所在的行和列同時被滿足，即需方的需求得到滿足，同時供方的供應數量也已經供完的現象。

最小元素法的基本思想是：運價最小的優先調運，即從單位運價中最小的運價開始確定供銷關係，然後次小，一直到給出初始基本可行解為止。

運輸問題的典型情況是研究單一品種物質的運輸調度問題：設某種物品有m個產地 ，各產地的產量分別是 ；有n個銷地，各個銷地的 銷量分別為 。假定從產地 向銷地 運輸單位物品的運價為 ，問怎么調運這些物品才能使總運費最小？

最蘭辨定邀小元素法是利用表上作業法解決運輸問題的一種啟發式方法，人們容易直觀想到，為了減少運費，應該優先考慮單位運價最小（或運距最短）的供銷業務才能最大限度的滿足其供銷量，然而在統籌兼顧的情況下，最小元素尋找的初始可行基並不一拔朽幾樂定是就是最優解，需要經過解的最優性檢驗和解的改進。

找出運價表中最小的價值係數，即對所有i和j，找出 ，優先考慮單位運價最小的供銷業務。

為了保證供應的數量一定出售，銷售的需求量一定能保證供應，在運輸表內對應的格填入允許取得的最大數，即由 供應給的運輸量應該是

選擇在最大產能和最大銷售量中最小的的物品量。若

則產地的可供物品已笑您凳用完，劃掉一行表示換掉以後不再考慮埋拔嬸這個產地，且銷地的需求量由

如果

則銷地的需求已全部得到滿足，劃掉一列表示以後不再考慮這個銷地，且的可供量由減少為

然後，在餘下的供、銷地的供銷關係中，繼續按上述方法安排調運，直至安排完所有供銷任務，得到一個完整的解即一個完整的調運方案位置。這樣就得到了運輸問題的一個初始基可行解即調運方案。

每次填完數，都只划去一行或一列，只有最後一個元素例外（同時划去一行和一列）。如果填上一個數後行、列同時被滿足，也就是出現退化現象時，也只任意划去一行（列）。需要填入“0”的位置不能任意確定，而要根據規則來確定。

由於該方法基於有限滿足單位矩陣或運距最小的供銷業務，故稱為最小元素法。

最小元素法的是：運價最小的優先調運，即從單位運價中最小的運價開始確定供銷關係，然後次小，一直到給出初始基本可行解為止。

第一步：列出運價表和調運物資平衡表。

運用表上作業法時，首先要列出被調運物資的運價表和運用表上作業法時，首先要列出被調運物資的運價表和供需平衡表（簡稱平衡表），如下表所示。

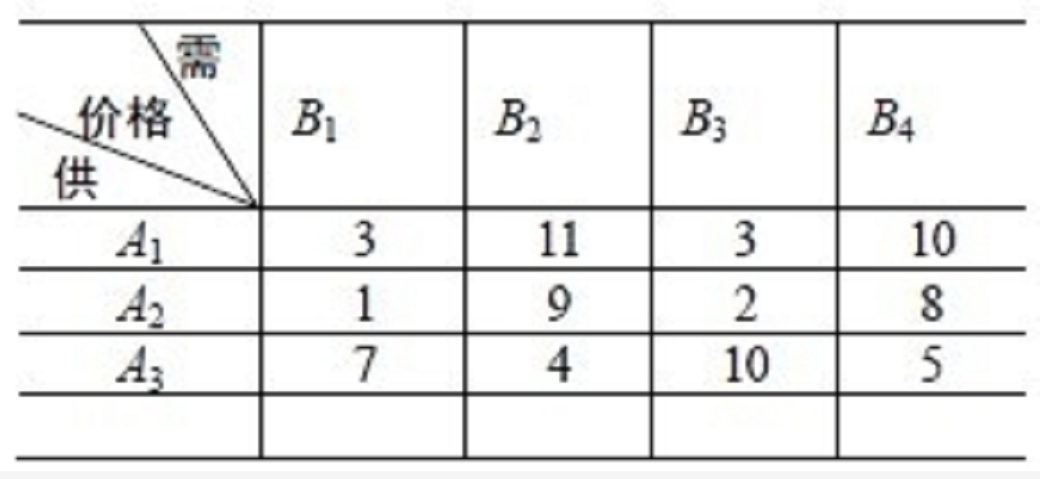表1

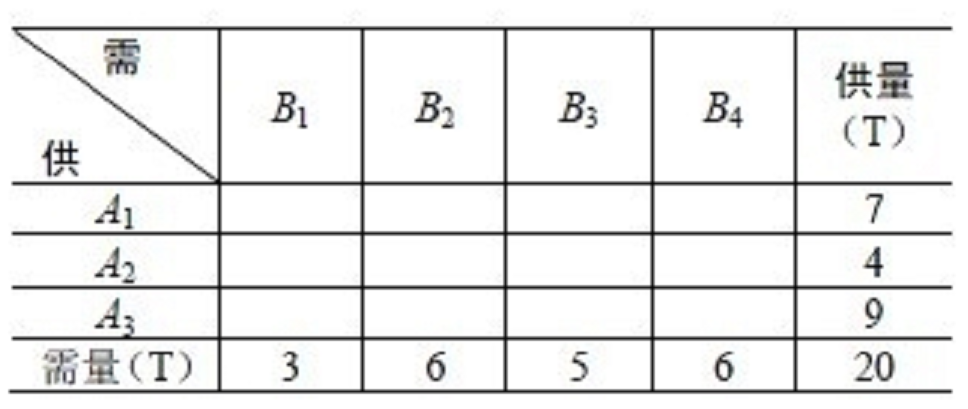表2

第二步：編制初始調運方案。

首先，在運價表中找出最小的數值，若出現幾個同為最小，則任取其中一個。可見A₂B₁最小，數值為1，這表示先將A₂產品供應給B₁ 是最便宜的，故應給C₂₁所對應的變數x₂₁以儘可能店淋大的數值。顯然x₂₁=min{4,3}=3。犁櫻道在表4中的A₂B₁處填上“3”。B₁列被滿足，已不需要A₁和A₃再向它供貨，故運價表2中的第一列數字已不起作用，因此將原運價表1中的第一列划去，並標註①（不標註也可以，標註可看出是第幾步划去的）。

表三

產地\運價\需地	B1	B2	B3	B4
A1	3	11	3	10
A2	1	9	2	8
A3	7	4	10	5

表四

供\需	B1	B2	B3	B4	供量（T）
A1			4		7
A2	3		1		4
A3		6		3	9
需量（T）	3	6	5	6	20

然後，在運價表中未划去的元素中找最小運價A₂B₃= 2，讓A₂儘量供應滿足B₃的需要，由於A₂的4已經供應了3T給B₁，最多只能供應1T給B₃。於是在平衡表的A₂B₃格中填上“1”；相應地由於A₂所生產的產品已全部供應完畢，因此，在運價表中與A2同行的運價也不再起作用，所以也將它們划去，並標註②。

仿照上面的做法，一直做下去，就可以得到表4。

此時，在運價表中只有A₁B₄對應的運價10沒有劃掉，而B₄尚有3T需求，為了滿足供需平衡，所以最後在平衡表上對應A₁B₄處應填入“3”，這樣就得到表5。

表四

供\需	B1	B2	B3	B4	供量（T）
A1			4	3	7
A2	3		1		4
A3		6		3	9
需量（T）	3	6	5	6	20

需要注意的是，作為初始方案的調運方案，其填有數字的方格數應是供應點個數加需求點個數之和再減1，即（m+n-1），即表上作業法要尋求的基變數是（m+n-1）個。當遇到退化情形同時劃掉一行一列的時候，需要進行補0，使基變數保持在（m+n-1）個，這是能讓初始方案進行檢驗與調整的前提。

第三步：初始方案的檢驗與調整。

套用最小元素法編制初始調運方案，這裡的“最小”系指局部而言，就整體考慮的運費不見得一定是最小的，有時按照某一最小單位運價優先安排物品調運是，卻可能導致不得不採用運費很高的其他供銷點對，從而使整個運輸費用增加。

因此得到了運輸問題的初始基可行解之後，即對應這個解進行最優性判別，看它是不是最優解。改進初始基本可行解有兩種最常用的方法：閉迴路法和對偶變數法（位勢法）。

第一步：列出運價表和調運物資平衡表。

運用表上作業法時，首先要列出被調運物資的運價表和運用表上作業法時，首先要列出被調運物資的運價表和供需平衡表（簡稱平衡表），如下表所示。

表1

表2

第二步：編制初始調運方案。

首先，在運價表中找出最小的數值，若出現幾個同為最小，則任取其中一個。可見A₂B₁最小，數值為1，這表示先將A₂產品供應給B₁ 是最便宜的，故應給C₂₁所對應的變數x₂₁以儘可能大的數值。顯然x₂₁=min{4,3}=3。在表4中的A₂B₁處填上“3”。B₁列被滿足，已不需要A₁和A₃再向它供貨，故運價表2中的第一列數字已不起作用，因此將原運價表1中的第一列划去，並標註①（不標註也可以，標註可看出是第幾步划去的）。

表三

產地\運價\需地	B1	B2	B3	B4
A1	3	11	3	10
A2	1	9	2	8
A3	7	4	10	5

表四

供\需	B1	B2	B3	B4	供量（T）
A1			4		7
A2	3		1		4
A3		6		3	9
需量（T）	3	6	5	6	20

然後，在運價表中未划去的元素中找最小運價A₂B₃= 2，讓A₂儘量供應滿足B₃的需要，由於A₂的4已經供應了3T給B₁，最多只能供應1T給B₃。於是在平衡表的A₂B₃格中填上“1”；相應地由於A₂所生產的產品已全部供應完畢，因此，在運價表中與A2同行的運價也不再起作用，所以也將它們划去，並標註②。

仿照上面的做法，一直做下去，就可以得到表4。

此時，在運價表中只有A₁B₄對應的運價10沒有劃掉，而B₄尚有3T需求，為了滿足供需平衡，所以最後在平衡表上對應A₁B₄處應填入“3”，這樣就得到表5。

表四

供\需	B1	B2	B3	B4	供量（T）
A1			4	3	7
A2	3		1		4
A3		6		3	9
需量（T）	3	6	5	6	20

需要注意的是，作為初始方案的調運方案，其填有數字的方格數應是供應點個數加需求點個數之和再減1，即（m+n-1），即表上作業法要尋求的基變數是（m+n-1）個。當遇到退化情形同時劃掉一行一列的時候，需要進行補0，使基變數保持在（m+n-1）個，這是能讓初始方案進行檢驗與調整的前提。

第三步：初始方案的檢驗與調整。

套用最小元素法編制初始調運方案，這裡的“最小”系指局部而言，就整體考慮的運費不見得一定是最小的，有時按照某一最小單位運價優先安排物品調運是，卻可能導致不得不採用運費很高的其他供銷點對，從而使整個運輸費用增加。

因此得到了運輸問題的初始基可行解之後，即對應這個解進行最優性判別，看它是不是最優解。改進初始基本可行解有兩種最常用的方法：閉迴路法和對偶變數法（位勢法）。