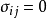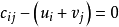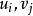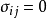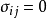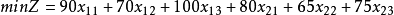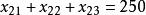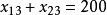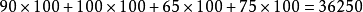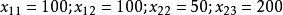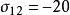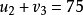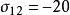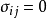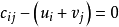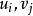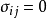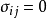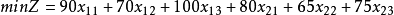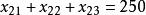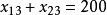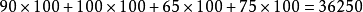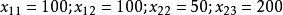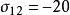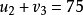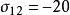表上作業法

表上作業法是指用列表的方法求解線性規劃問題中運輸模型的計算方法。是線性規劃一種求解方法，其實質是單純形法，故也稱運輸問題單純形法。當某些線性規劃問題採用圖上作業法難以進行直觀求解時，就可以將各元素列成表格，作為初始方案，然後採用檢驗數來驗證這個方案，否則就要採用閉合迴路法、位勢法等方法進行調整，直至得到滿意的結果。這種列表求解方法就是表上作業法。

基本介紹

• 中文名：表上作業法
• 外文名：Table on the operating method
• 領域：運籌學
• 屬性：用列表的方法求解線性規劃問題
• 實質：單純形法
• 相關名詞：圖上作業法

定義

表上作業法是指用列表的方法求解線性規劃問題中運輸模型的計算方法。是線性規劃一種求解方法，其實質是單純形法，故也稱運輸問題單純形法。當某些線性規劃問題採用圖上作業法難以進行直觀求解時，就可以將各元素列成表格，作為初始方案，然後採用檢驗數來驗證這個方案，否則就要採用閉合迴路法、位勢法等方法進行調整，直至得到滿意的結果。這種列表求解方法就是表上作業法。

作業法的步驟

1、找出初始基本可行解（初始調運方案，一般m+n-1個數字格），用西北角法、最小元素法；

（1）西北角法：

從西北角（左上角）格開始，在格內的右下角標上允許取得的最大數。然後按行（列）標下一格的數。若某行（列）的產量（銷量）已滿足，則把該行（列）的其他格划去。如此進行下去，直至得到一個基可行解。

（2）最小元素法

從運價最小的格開始，在格內的右下角標上允許取得的最大數。然後按運價從小到大順序填數。方法同西北角法。

注:套用西北角法和最小元素法，每次填完數，都只划去一行或一列，只有最後一個元例外（同時划去一行和一列）。當填上一個數後行、列同時飽和時，也應任意划去一行（列），在保留的列（行）中沒被划去的格內標一個0。

2、求出各非基變數的檢驗數，判別是否達到最優解。如果是停止計算，否則轉入下一步，用位勢法計算；

運輸問題的約束條件共有m+n個，其中：m是產地產量的限制；n是銷地銷量的限制。其對偶問題也應有m+n個變數，據此：

，其中前m個計為 ，前n個計為

由單純形法可知，基變數的

，因此 可以求出。

3、改進當前的基本可行解（確定換入、換出變數），用閉合迴路法調整；

（因為目標函式要求最小化）

表格中有調運量的地方為基變數，空格處為非基變數。基變數的檢驗數 ，非基變數的檢驗數 。 表示運費減少， 表示運費增加。

4、重複②，③，直到找到最優解為止。

常見問題

1、無窮多最優解

產銷平衡的運輸問題必定存最優解。如果非基變數的 ，則該問題有無窮多最優解。

2、退化

表格中一般要有(m+n-1)個數字格。但有時，在分配運量時則需要同時划去一行和一列，這時需要補一個0，以保證有(m+n-1)個數字格。一般可在划去的行和列的任意空格處加一個0即可。

相關關係

（1）運輸問題的求解採用表上作業法，即用列表的方法求解線性規劃問題中的運輸模型的計算方法，實質上是單純形法。表上作業法是一種特定形式的單純形法，它與單純形法有著完全相同的解題步驟，所不同的只是完成各步採用的具體形式；

（2）表上作業法中的最小元素法和伏格爾法實質上是在求單純形表中的初始基可行解；

（3）表上作業法中的“位勢法”實質上是在求單純形表中的檢驗數；

（4）調運方案表中數字格的數實質上就是單純形法中基變數的值；

（5）調運方案表上的“閉迴路法”實質上是在做單純形表上的換基疊代。

舉例

甲、乙兩個煤礦供應A、B、C三個城市用煤，各煤礦產量及各城市需煤量、各煤礦到各城市的運輸單價見表所示，求使總運輸費用最少的調運方案。

總運輸量：

日產量約束：

需求約束：

最小元素

法用最小元素法確定初始調運方案：

總運價為：

西北角法

用西北角法確定初始調運方案：

總運價為：

最優性檢驗

1、閉迴路法：

（1）思路：要判定運輸問題的初始基可行解是否為最優解，可仿照一般單純形法，檢驗這個解的各非基變數（對應於運輸表中的空格）的檢驗數。

（2）檢驗數：運輸問題中非基變數（對應於空格）的檢驗數定義為給某空格增加單位運量導致總費用的增加量。

（3）如果有某空格 的檢驗數為負，說明將 變為基變數將使運輸費用減少，故當前這個解不是最優解。若所有空格的檢驗數全為非負，則不管怎樣變換，均不能使運輸費用降低，即目標函式值已無法改進，這個解就是最優解。

閉迴路：在給出的調運方案的運輸表上，從一個空格（非基變數）出發，沿水平或垂直方向前進，只有碰到代表基變數的數字格才能向左或向右轉90°繼續前進，直至最終回到初始空格而形成的一條迴路。 從每一空格出發，一定可以找到一條且只存在唯一一條閉迴路 。

以 空格為第一個奇數頂點，沿閉迴路的順（或逆）時針方向前進，對閉迴路上的每個折點依次編號；

非基變數 xij 的檢驗數：

=（閉迴路上奇數次頂點運距或運價之和）-（閉迴路上偶數次頂點運距或運價之和） 。

現在，在用最小元素法確定初始調運方案的基礎上，計算非基變數X₁₂的檢驗數 ：

非基變數X₁₂的檢驗數： ；非基變數X₂₁的檢驗數：

2、對偶變數法（位勢法）

以初始調運方案為例，設定對偶變數 和 ，然後構造下面的方程組：

在式中，令u₁=0，可解得其他量進而求出；。與前面用閉迴路法求得的結果相同。

解的改進

如檢驗出初始解不是最優解，即某非基變數檢驗數為負，說明將這個非基變數變為基變數時運費會下降。根據表上作業法的第三步，需對初始方案進行改進。

解改進的步驟為：

1．（如存在多個非基變數的檢驗數為負時，以最小負檢驗數所在空格對應的變數）為換入變數，找出它在運輸表中的閉迴路；

2．以這個空格為第一個奇數頂點，沿閉迴路的順（或逆）時針方向前進，對閉迴路上的每個折點依次編號；

3．在閉迴路的所有偶數折點中，找出運輸量最小的一個折點，以該格中的變數為換出變數；

4．將閉迴路上所有奇數折點的運輸量都增加這一換出變數值，所有偶數折點處的運輸量都減去這一數值，最終得出一個新的運輸方案。 對得出的新方案再進行最優性檢驗，如不是最優解，就重複以上步驟繼續進行調整，一直到得出最優解為止。

因σ₁₂=-20 ，畫出以x₁₂為起始變數的閉迴路，計算調整量；

按照下面的方法調整調運量：

（1）閉迴路上，奇數次頂點的調運量加上ε，偶數次頂點的調運量減去ε；

（2）閉迴路之外的變數調運量不變。

得到新的調運方案：

最優調運方案是：

相應的最小總運輸費用為：