主要內容
曲線回歸分析方法的主要內容有:
① 確定兩個變數間數量變化的某種特定的規則或
規律;
② 估計表示該種曲線關係特點的一些重要
參數,如回歸參數、極大值、極小值和漸近值等;
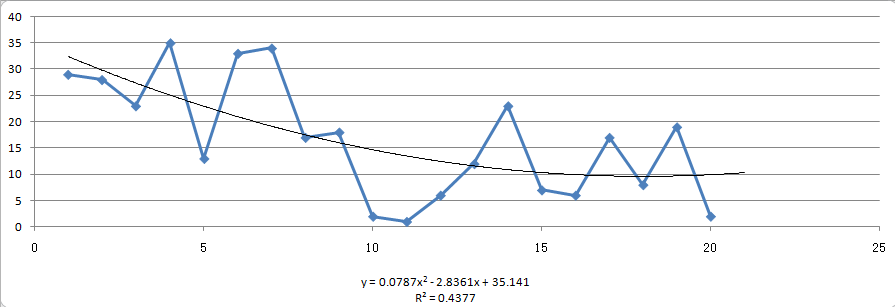 圖1.曲線回歸舉例
圖1.曲線回歸舉例③ 為生產預測或試驗控制進行
內插,或在論據充足時作出理論上的外推。
分類
曲線方程配置(curve fitting):是指對兩個變數資料進行曲線
回歸分析,獲得一個顯著的曲線方程的過程。按照曲線方程的配置主要可以分為以下四類:
1)曲線回歸分析的一般程式;
4)Logistic曲線方程。
操作步驟
1.Excel步驟
1、將數據輸入excel表格中,行表示或列表示均可。
2、選定數據區域,然後單擊工具列中的“
圖表嚮導”(或在選單欄單擊“插入”-“圖表”),彈出
對話框,選擇“xy
散點圖”,再選擇子圖表中的第一個
散點圖。
3、按“下一步”,大概的圖就完成了,它會讓你選擇所產生的數據是“行”或“列”,根據你的要求選擇。再點擊下一步,可以將行或列的標題內容填入。接著點擊“下一步”之後點“完成”。圖表就完成了。
4、選擇圖表上的任意一個點(選中一個點之後,其餘的點都變為黃色了),單擊右鍵,選擇“添加趨勢線”。在“添加趨勢線”
對話框中的“類型”選“
線性”,在“選項”中把“顯示公式”和“顯示R平方值”點上,如果你不想設定截距,就不用點擊“設定截距”。
 圖2.常用的曲線圖
圖2.常用的曲線圖2.spss操作步驟
基本原理:
線性回歸不能解決所有問題,儘管有可能通過一些函式的轉換,在一定範圍內將因變數,自變數之間的關係轉化為線性關係,但是,這種轉換有可能導致更複雜的計算或者失真。如果線性模型不能確定哪一種為最佳,就需要嘗試曲線擬合的方法。這樣能建立一個簡單並且合適的模型。
要求:
自變數可以為一個或者多個,因變數只能為一個。如果自變數為時間變數,可以在“保存”對話框的“預測觀測量”欄指定一種超出當前數據時間序列範圍的預測周期。意思就是用已經有了的時間預測未來。但是,首先需要在此欄中設定。系統會根據設定的時間自動進行預測。
從估計期到最後一個個案預測”如果沒有指定這個選項,系統默認使用所有的觀測量。但是,如果指定,就使用指定的觀測量,意思就是讓你根據需要篩選個案值。
預測範圍:
根據預先設定的周期,對特定的數據,在指定的時間內進行預測。也就是需要選擇一個超出時間變數的所有觀測量的範圍,這個超出的時間才有資格成為預測範圍,這就是需要人腦分析並根據實際需要,設定一個未來的範圍,系統就會根據設定的這個未來範圍進行分析,得出結果。
結果:
1 方差分析表:此表是每一個模型具有一個,只要選擇,就分別在主對話框已經選擇的模型輸出。如果小於95%置信區間的小機率0.05,就說明有統計意義,這個模型有希望,能夠進行擬合。反之亦然。
2 R方和調整R方:如果二者越接近1說明模型的擬合效果越好。
3 圖形:從此圖中可以一目了然哪種模型最好,也就是哪種模型和所有的散點越接近。
4係數:根據非標準化係數,和它對應的變數,即可寫出相應的曲線回歸方程。
5 殘差:一個補充的判斷最優模型的方法。
結果圖形判斷方法:最平穩的就是最合適的方程。
 圖1.曲線回歸舉例
圖1.曲線回歸舉例 圖2.常用的曲線圖
圖2.常用的曲線圖
