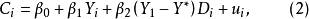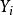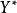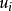分段線性回歸是指當y對x的回歸在x的某一範圍的服從某種線性關係,在其他範圍內又服從斜率不同的線性關係時適用的一種回歸估計方法。這種方法使用指示變數對各段(即不同範圍的)數據同時擬合統—的回歸模型。
基本介紹
- 中文名:分段線性回歸
- 外文名:piecewise linear regression
- 所屬學科:數學(統計學)
- 相關概念:虛擬變數,解釋變數,回歸方程等
基本介紹,模型分析,舉例分析,
基本介紹
虛擬變數可以代表質的因素,有些情況下,虛擬變數也可以代表數量因素。分段線性回歸就是類似情形中常見的一種。
在經濟關係中常有這樣的情況:當解釋變數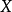 的值達到某一水平
的值達到某一水平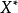 之前,與被解釋變數
之前,與被解釋變數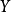 之間存在某種線性關係;當解釋變數
之間存在某種線性關係;當解釋變數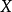 的值達到或超過
的值達到或超過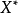 以後,與被解釋變數的關係就會發生變化。此時,如果已知
以後,與被解釋變數的關係就會發生變化。此時,如果已知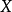 的轉折點
的轉折點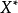 。我們就可以用虛擬變數來估計每一段的斜率。這就是所謂的分段線性回歸。
。我們就可以用虛擬變數來估計每一段的斜率。這就是所謂的分段線性回歸。
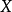
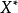
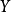
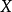
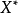
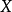
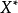
模型分析
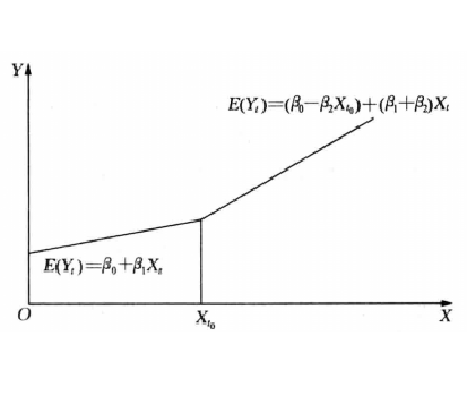
分段線性回歸模型由兩條直線組成,但在折點處曲線仍是連續的。考慮以下的基本模型:
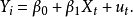
假定因變數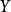 和解釋變數
和解釋變數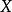 均呈現隨時間穩定增長的趨勢,在時間
均呈現隨時間穩定增長的趨勢,在時間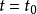 處反映兩者之間關係的曲線出現轉折,使得兩段曲線的截距和斜率都發生變化,但
處反映兩者之間關係的曲線出現轉折,使得兩段曲線的截距和斜率都發生變化,但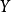 的變化具有連續性。我們設定以下形式的虛擬變數:
的變化具有連續性。我們設定以下形式的虛擬變數:
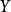
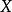
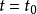
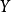
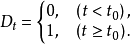
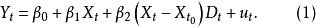
由式(1) 可以看出,當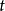 處於不同時間段時,
處於不同時間段時,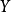 的期望值分別為
的期望值分別為
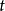
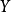
當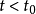 時,有
時,有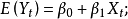
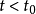
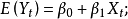
當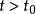 時,有
時,有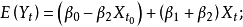
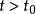
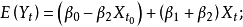
當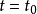 時,有
時,有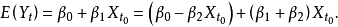
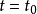
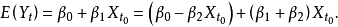
即在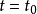 處曲線為連續的,圖1反映出這一情況。
處曲線為連續的,圖1反映出這一情況。 圖1 分段線性回歸模型
圖1 分段線性回歸模型
 圖1 分段線性回歸模型
圖1 分段線性回歸模型舉例分析
在研究實際經濟問題時,有些經濟變數之間的因果關係會在解釋變數達到某個臨界值時發生突變,為了區分這種變化,可以利用虛擬變數進行分段線性回歸。
例如,根據消費理論,消費水平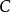 主要取決於收入水平
主要取決於收入水平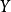 ;假設高收入與低收入人群的消費傾向存在差異,則這種消費傾向的差異可通過在收入的係數中引入虛擬變數來考察,建立如下消費模型:
;假設高收入與低收入人群的消費傾向存在差異,則這種消費傾向的差異可通過在收入的係數中引入虛擬變數來考察,建立如下消費模型:
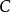
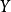
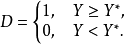
低收入人群
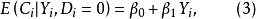
高收入人群
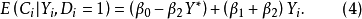
式(3)和式(4)分別表示低收入人群和高收入人群的消費函式;不同收入人群的消費行為是否存在顯著差異,可以通過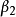 的統計顯著性檢驗進行判斷。
的統計顯著性檢驗進行判斷。
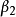
如圖2所示,模型(2)實際上是將兩段回歸合併進行,這兩段回歸不僅截距不同,而且斜率不同。分兩段線性回歸引入了一個虛擬變數;容易推廣,分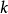 段線性回歸應引入了
段線性回歸應引入了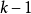 個虛擬變數。
個虛擬變數。 圖2 不同收入人群的消費差異
圖2 不同收入人群的消費差異
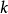
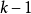
 圖2 不同收入人群的消費差異
圖2 不同收入人群的消費差異