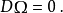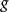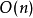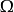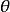曲率形式

微分幾何中，曲率形式（curvature form）描述了主叢上的聯絡的曲率。它可以看作是黎曼幾何中的曲率張量的替代或是推廣。

基本介紹

• 中文名：曲率形式
• 外文名：curvature form
• 套用學科：數學
• 所屬領域：幾何學
• 定義：是特徵曲率張量的二次形式
• 相關術語：比安基恆等式

定義

曲率形式(curvature forms)是特徵曲率張量的二次形式。

令G為一個李群，記G的李代數為 。設 為一個主G-叢。令 表示E上一個埃雷斯曼聯絡（它是一個E上的g-值1-形式）。

那么曲率形式就是E上的g-值 2-形式，定義為

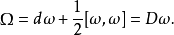
這裡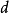 表示標準外導數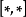， 是李括弧，而D表示外共變導數。或者說

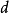
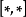
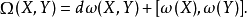
表示

向量叢上的曲率形式

若 是一個纖維叢，其結構群為G，我們可以在相伴的主G-叢上重複同樣的定義。

若 是一個向量叢則我們可以把 看作是 1-形式的矩陣，則上面的公式取如下形式：

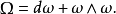
其中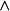 是楔積。更準確地講，若 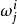和 分別代表 和 的分量（所以每個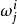 是一個通常的 1-形式而每個 是一個普通的2-形式），則

例如，黎曼流形的切叢，我們有 作為結構群而 是在 中取值的 2-形式（給定標準正交基，可以視為反對稱矩陣）。在這種情況， 是曲率張量的一種替換表述，也就是在曲率張量的標準表示中，我們有

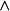
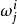
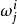
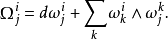
上式使用了黎曼曲率張量標準記號。

相關拓展

比安基恆等式

如果 是標架叢上的典範向量值 1-形式，聯絡形式 ω 的撓率是由結構方程定義的向量值 2-形式：

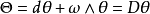
這裡D代表外共變導數。

第一比安基恆等式（對於標架叢的有撓率聯絡）取以下形式：

第二比安基恆等式對於一般有聯絡的叢成立，並有如下形式：