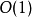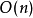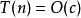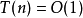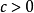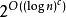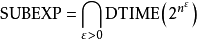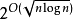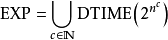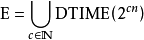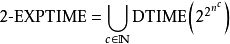簡介,算法複雜度,常數時間,對數時間,冪對數時間,次線性時間,線性時間,線性對數時間,多項式時間,超越多項式時間,準多項式時間,次指數時間,第一定義,第二定義,指數時間,雙重指數時間,
簡介
為了計算時間複雜度,我們通常會估計算法的操作單元數量,每個單元運行的時間都是相同的。因此,總運行時間和算法的操作單元數量最多相差一個常量係數。
相同大小的不同輸入值仍可能造成算法的運行時間不同,因此我們通常使用算法的最壞情況複雜度,記為T(n),定義為任何大小的輸入n所需的最大運行時間。另一種較少使用的方法是平均情況複雜度,通常有特別指定才會使用。時間複雜度可以用函式T(n) 的自然特性加以分類,舉例來說,有著T(n) =O(n) 的算法被稱作“線性時間算法”;而T(n) =O(M) 和M= O(T(n)) ,其中M≥n> 1 的算法被稱作“指數時間算法”。
一個算法花費的時間與算法中語句的執行次數成正比例,哪個算法中語句執行次數多,它花費時間就多。一個算法中的語句執行次數稱為語句頻度或時間頻度。記為T(n)。
一般情況下,算法中基本操作重複執行的次數是問題規模n的某個函式,用T(n)表示,若有某個輔助函式f(n),使得當n趨近於無窮大時,T(n)/f (n)的極限值為不等於零的常數,則稱f(n)是T(n)的同數量級函式。記作T(n)=O(f(n)),稱O(f(n)) 為算法的漸進時間複雜度,簡稱時間複雜度。
在各種不同算法中,若算法中語句執行次數為一個常數,則時間複雜度為O(1),另外,在時間頻度不相同時,時間複雜度有可能相同,如T(n)=n2+3n+4與T(n)=4n2+2n+1它們的頻度不同,但時間複雜度相同,都為O(n2)。
時間頻度
一個算法執行所耗費的時間,從理論上是不能算出來的,必須上機運行測試才能知道。但我們不可能也沒有必要對每個算法都上機測試,只需知道哪個算法花費的時間多,哪個算法花費的時間少就可以了。並且一個
算法花費的時間與算法中語句的執行次數成正比例,哪個算法中語句執行次數多,它花費時間就多。一個
算法中的語句執行次數稱為語句頻度或時間頻度。記為T(n)。
算法複雜度
常數時間
若對於一個算法,
的上界與輸入大小無關,則稱其具有
常數時間,記作
時間。一個例子是訪問
數組中的單個元素,因為訪問它只需要一條
指令。但是,找到無序數組中的最小元素則不是,因為這需要遍歷所有元素來找出最小值。這是一項線性時間的操作,或稱
時間。但如果預先知道元素的數量並假設數量保持不變,則該操作也可被稱為具有常數時間。
雖然被稱為“常數時間”,運行時間本身並不必須與問題規模無關,但它的上界必須是與問題規模無關的確定值。舉例,“如果a > b則交換a、b的值”這項操作,儘管具體時間會取決於條件“a > b”是否滿足,但它依然是常數時間,因為存在一個常量t使得所需時間總不超過t。
以下是一個常數時間的代碼片段:
int index = 5;int item = list[index];if (condition true) then perform some operation that runs in constant timeelse perform some other operation that runs in constant timefor i = 1 to 100 for j = 1 to 200 perform some operation that runs in constant time
對數時間
若算法的
T(
n) =
O(logn),則稱其具有
對數時間。由於計算機使用
二進制的記數系統,
對數常常以2為底(即log
2n,有時寫作lg
n)。然而,由對數的
換底公式,log
an和log
bn只有一個常數因子不同,這個因子在大O記法中被丟棄。因此記作O(log
n),而不論對數的底是多少,是對數時間算法的標準記法。
常見的具有對數時間的算法有
二叉樹的相關操作和二分搜尋。
對數時間的算法是非常有效的,因為每增加一個輸入,其所需要的額外計算時間會變小。
遞歸地將字元串砍半並且輸出是這個類別函式的一個簡單例子。它需要O(log n)的時間因為每次輸出之前我們都將字元串砍半。 這意味著,如果我們想增加輸出的次數,我們需要將字元串長度加倍。
// 遞歸輸出一個字元串的右半部分var right = function(str){ var length = str.length; // 輔助函式 var help = function(index) { // 遞歸情況:輸出右半部分 if(index < length){ // 輸出從index到數組末尾的部分 console.log(str.substring(index, length)); // 遞歸調用:調用輔助函式,將右半部分作為參數傳入 help(Math.ceil((length + index)/2)); } // 基本情況:什麼也不做 } help(0);}冪對數時間
對於某個常數
k,若算法的
T(
n) = O((log
n)),則稱其具有
冪對數時間。例如,矩陣鏈排序可以通過一個
PRAM模型.被在冪對數時間內解決。
次線性時間
對於一個算法,若其匹配T(n) = o(n),則其時間複雜度為次線性時間(sub-linear time或sublinear time)。實際上除了匹配以上定義的算法,其他一些算法也擁有次線性時間的時間複雜度。例如有O(n)葛羅佛搜尋算法。
常見的非合次線性時間算法都採用了諸如平行處理(就像NC1matrix行列式計算那樣)、非古典處理(如同葛羅佛搜尋那樣),又或者選擇性地對有保證的輸入結構作出假設(如冪對數時間的二分搜尋)。不過,一些情況,例如在頭 log(n) 比特中每個字元串有一個比特作為索引的字元串組就可能依賴於輸入的每個比特,但又匹配次線性時間的條件。
“次線性時間算法”通常指那些不匹配前一段的描述的算法。它們通常運行於傳統計算機架構系列並且不容許任何對輸入的事先假設。但是它們可以是
隨機化算法,而且必須是真隨機算法除了特殊情況。
線性時間
如果一個算法的時間複雜度為O(n),則稱這個算法具有線性時間,或O(n)時間。非正式地說,這意味著對於足夠大的輸入,運行時間增加的大小與輸入成線性關係。例如,一個計算列表所有元素的和的程式,需要的時間與列表的長度成正比。這個描述是稍微不準確的,因為運行時間可能顯著偏離一個精確的比例,尤其是對於較小的n。
線性對數時間
若一個算法時間複雜度T(n) = O(nlog n),則稱這個算法具有線性對數時間。因此,從其表達式我們也可以看到,線性對數時間增長得比線性時間要快,但是對於任何含有n,且n的冪指數大於1的多項式時間來說,線性對數時間卻增長得慢。
多項式時間
複雜度類
從
多項式時間的概念出發,在計算複雜度理論中可以得到一些複雜度類。以下是一些重要的例子。
ZPP:包含可以使用機率圖靈機在多項式時間內零錯誤解決的決定性問題。
RP:包含可以使用機率圖靈機在多項式時間內解決的決定性問題,但它給出的兩種答案中(是或否)只有一種答案是一定正確的,另一種則有幾率不正確。
BPP:包含可以使用機率圖靈機在多項式時間內解決的決定性問題,它給出的答案有錯誤的機率在某個小於0.5的常數之內。
BQP:包含可以使用量子圖靈機在多項式時間內解決的決定性問題,它給出的答案有錯誤的機率在某個小於0.5的常數之內。
在機器模型可變的情況下,
P在確定性機器上是最小的時間複雜度類。例如,將單帶圖靈機換成多帶圖靈機可以使算法運行速度以二次階提升,但所有具有多項式時間的算法依然會以多項式時間運行。一種特定的
抽象機器會有自己特定的複雜度類分類。
超越多項式時間
如果一個算法的時間T(n) 沒有任何多項式上界,則稱這個算法具有超越多項式(superpolynomial)時間。在這種情況下,對於所有常量c我們都有T(n) = ω(n),其中n是輸入參數,通常是輸入的數據量(比特數)。指數時間顯然屬於超越多項式時間,但是有些算法僅僅是很弱的超越多項式算法。例如,Adleman-Pomerance-Rumely 質數測試對於n比特的輸入需要運行n時間;對於足夠大的n,這時間比任何多項式都快;但是輸入要大得不切實際,時間才能真正超過低級的多項式。
準多項式時間
準多項式時間算法是運算慢於多項式時間的算法,但不會像指數時間那么慢。對一些固定的
,準多項式時間算法的最壞情況運行時間是
。如果準多項式時間算法定義中的常量“c”等於1,則得到多項式時間算法;如果小於1,則得到一個次線性時間算法。
次指數時間
術語次指數時間用於表示某些算法的運算時間可能比任何多項式增長得快,但仍明顯小於指數。在這種狀況下,具有次指數時間算法的問題比那些僅具有指數算法的問題更容易處理。“次指數”的確切定義並沒有得到普遍的認同,我們列出了以下兩個最廣泛使用的。
第一定義
如果一個問題解決的運算時間的對數值比任何多項式增長得慢,則可以稱其為次指數時間。更準確地說,如果對於每個 ε> 0,存在一個能於時間 O(2) 內解決問題的算法,則該問題為次指數時間。所有這些問題的集合是複雜性SUBEXP,可以按照DTIME的方式定義如下。
第二定義
一些作者將次指數時間定義為 2的運算時間。該定義允許比次指數時間的第一個定義更多的運算時間。這種次指數時間算法的一個例子,是用於整數因式分解的最著名古典算法——
普通數域篩選法,其運算時間約為
,其中輸入的長度為
n。另一個例子是圖形同構問題的最著名算法,其運算時間為
。
指數時間
若
T(
n) 是以 2為上界,其中 poly(
n) 是
n的多項式,則算法被稱為
指數時間。更正規的講法是:若
T(
n) 對某些常量
k是由 O(2) 所界定,則算法被稱為
指數時間。在確定性圖靈機上認定為指數時間算法的問題,形成稱為
EXP的複雜性級別。
有時侯,指數時間用來指稱具有
T(
n) = 2的算法,其中指數最多為
n的線性函式。這引起複雜性檔次
E。
雙重指數時間
若T(n) 是以 2為上界,其中 poly(n) 是n的多項式,則算法被稱為雙重指數時間。這種算法屬於複雜性檔次2-EXPTIME。
眾所周知的雙重指數時間算法包括: