在計算複雜性理論中,BQP(bounded-error quantum polynomial time)是量子計算機在多項式時間內可以解決的一類決策問題,所有實例的錯誤機率至多為1/3。它是複雜類BPP的量子類比。
基本介紹
- 外文名:bounded-error quantum polynomial time
- 縮寫:BQP
介紹,量子計算,與其他複雜類的關係,
介紹


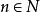

對於全部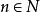 ,
, 取
取 個比特作為輸入並輸出1比特;
個比特作為輸入並輸出1比特;
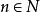


對於L中的所有x, ;
;

對於L中的所有x, .
.

量子計算
計算機中的量子比特數允許為實例大小的多項式函式。 例如,已知用僅超過2n個量子位(Shor算法)來分解n位整數的算法。
通常,量子計算機上的計算以測量結束。 這導致量子態向基態的崩潰。 可以說量子態被測量的機率很高,處於正確的狀態。
量子計算機已經引起了廣泛的興趣,因為已知一些實際感興趣的問題在 中,但被懷疑在
中,但被懷疑在 之外。一些突出的例子是:
之外。一些突出的例子是:


a.整數因子分解(參見Shor算法);
b.離散對數;
c.量子系統的模擬(見通用量子模擬器);
d.在統一的某個根逼近瓊斯多項式;
b.離散對數;
c.量子系統的模擬(見通用量子模擬器);
d.在統一的某個根逼近瓊斯多項式;
與其他複雜類的關係
該類是為量子計算機定義的,其普通計算機(或圖靈機加隨機源)的自然對應類是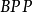 。就像
。就像 和
和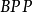 一樣,
一樣, 本身就很低,這意味著
本身就很低,這意味著 =
= 。非正式地說,這是因為多項式時間算法在組合下是閉合的。如果一個多項式時間算法作為子程式調用多項式多項式時間算法,則所得到的算法仍然是多項式時間。
。非正式地說,這是因為多項式時間算法在組合下是閉合的。如果一個多項式時間算法作為子程式調用多項式多項式時間算法,則所得到的算法仍然是多項式時間。
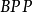

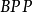





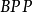







由於 的問題還沒有解決,
的問題還沒有解決, 和上述類別之間不平等的證明應該是困難的。
和上述類別之間不平等的證明應該是困難的。 和
和 之間的關係尚不清楚。
之間的關係尚不清楚。




將後期選擇添加到 會導致複雜性類Post
會導致複雜性類Post 於
於 。
。



